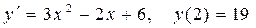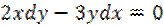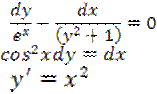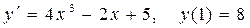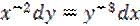Определение. Уравнение (1) называется однородным, если может быть представлена как функция отношения своих аргументов, т.е. (2) .

Таким образом, однородное уравнение имеет вид: (3)

Теорема. Однородное уравнение (3) имеет общий интеграл: .

Определение. Линейным дифференциальным уравнением I порядка называется дифференциальное уравнение вида: 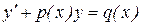(1),

где – неизвестная функция аргумента.

Уравнение (1) линейно относительно и . Если , то уравнение (1) примет вид: (2), и называется линейным однородным.

2. Методические рекомендации по решению упражнений и задач.

1) Пример.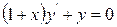

Решение: приведем уравнение к виду (1) (учитывая, что ):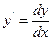

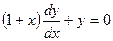
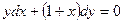
В данном уравнении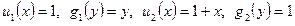

Разделяя переменные, получим:

Интегрируя, найдем общий интеграл:

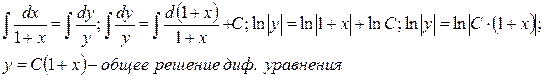
2) Пример 2: Найти частное решение дифференциального уравнения, удовлетворяющего начальным условиям

;

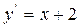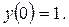
Решение: Приведем уравнение к виду (1) и разделим переменные:

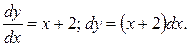
Интегрируя, найдем общий интеграл:

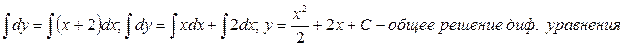
Т.к. 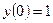, то подставляя это начальное условие в общее решение диф. уравнения, найдем значение С:

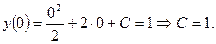
Значит частное решение данного диф. уравнения имеет вид:

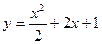3. Задания самостоятельной работы.

1 вариант 2 вариант

Решить дифференциальные уравнения с разделяющимися переменными

4. .

5. Решить задачу Коши:

Решить дифференциальные уравнения с разделяющимися переменными

5. Решить задачу Коши:

4. Контрольные вопросы

1. Какое дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными?

2. Как решается дифференциальное уравнение с разделяющимися переменными?

3. Сформулируйте задачу Коши.