Упрощение логических выражений

Упрощение логических выражений

Логические уравнения

Если приравнять два логических выражения, мы получим уравнение. Его решением будут значения переменных, при которых уравнение превращается в истинное равенство, т. е. когда значения левой и правой частей совпадают. Например, уравнение А • В = 1 имеет единственное решение: А = В = 1, для остальных комбинаций значений переменных левая часть равна нулю. В то же время уравнение А + В = 1 имеет три решения: (А = 0, В = 1), (А = 1, В = 0) и А = В = 1.

Пример 1. Требуется найти все решения уравнения

(не (B + C) • А) → (не А • не C + D) = 0.

Вспоминаем, что импликация равна нулю только тогда, когда первое выражение равно 1, а второе — 0. Поэтому исходное уравнение сразу разбивается на два:

Не (B + C) • А = 1, не А • C + не D = 0.

Первое уравнение с помощью закона де Моргана можно преобразовать к виду: не В • не C • А = 1, откуда сразу следует, что все три сомножителя должны быть равны 1. Это значит, что А = 1, В = 0 и С = 0. Кроме того, из второго уравнения следует, что В=0. А=1 и С = 0 удовлетворяют и второму уравнению тоже. Решение найдено, причём оно единственное.

Возможен второй вариант — упростить выражение. Заменяя импликацию по формуле А → В = не А + В получаем:

Не (B + C) • A + не А • C + D = 0.

Используем закон де Моргана:

B + C + не А + не А •не C + D = 0.

и закон поглощения:

В + С + не А + D =0.

Для того чтобы логическая сумма была равна нулю, каждое слагаемое должно быть равно нулю, поэтому А = 1, В = С = D = 0.

Есть и третий вариант — построить таблицу истинности выражения в левой части и найти все варианты, при которых оно равно 0. Однако таблица истинности выражения с четырьмя переменными содержит 2⁴ = 16 строк, поэтому такой подход достаточно трудоёмок.

Для тех, кто претендует на 4 или 5, самостоятельно: Построить Таблицу Истинности (для четырех переменных)!

Пример 2. Требуется найти все решения уравнения

(А + не В) → (В • С • D) = 1.

Преобразуем выражение, раскрыв импликацию через операции «НЕ» и «ИЛИ» и применив закон де Моргана:

не (А +не В)+ В • С • D = не А • В + В • С • D= 1.

Если логическая сумма равна 1, то хотя бы одно слагаемое равно 1 (или оба одновременно).

Равенство не А • В = 1 верно при А = 0, В = 1 и любых С и В. Поскольку есть всего 4 комбинации значений С и D, уравнение А • В = 1 имеет 4 решения:

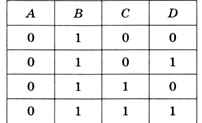
Второе уравнение, B • C • D=1, даёт В = С = D = 1 при любом А, т. е. оно имеет два решения:

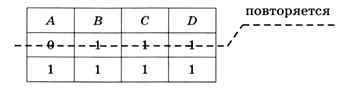
Видим, что первое из этих решений уже было получено раньше, поэтому уравнение имеет всего пять разных решений. Заметим, что определить все повторяющиеся решения можно из уравнения (А • В) • (B • C • D) = 1, которое имеет единственное решение А = 0, В = С = D = 1.

Пример 3. Требуется найти число решений уравнения

A • B • C + не B • не C • D = 0..

Здесь, в отличие от предыдущих задач, не нужно находить сами решения, интересует только их количество. Уравнение распадается на два:

A • B • C = 0 и не B • не C • D = 0.

Каждое из них имеет достаточно много решений. Можно поступить следующим образом: сначала найти количество решений «обратного» уравнения, с единицей в правой части:

12 Следующая ⇒