Представление графов. Матрица смежности

Представление графов

Существует два способа представления графа, в виде списков смежности и в виде матрицы смежности. Оба способа подходят для представления ориентированных и неориентированных графов.

Матрица смежности

Этот способ является удобным для представления плотных графов, в которых количество рёбер (|E|) примерно равно количеству вершин в квадрате (|V|²).
В данном представлении мы заполняем матрицу размером |V| x |V| следующим образом:
A[i][j] = 1 (Если существует ребро из i в j)

A[i][j] = 0 (Иначе)

Данный способ подходит для ориентированных и неориентированных графов. Для неориентированных графов матрица A является симметричной (то есть A[i][j] == A[j][i], т.к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
Понятно что с помощью данного способа представления, можно быстро проверить есть ли ребро между вершинами v и u, просто посмотрев в ячейку A[v][u]. С другой стороны этот способ очень громоздкий, так как требует O (|V|²) памяти для хранения матрицы.

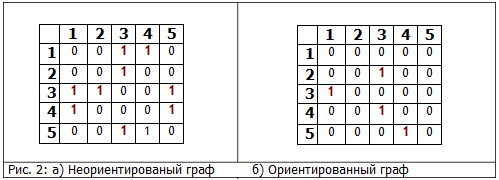
На рис. 2 приведены представления графов из рис. 1 с помощью матриц смежности.

Списки смежности

Данный способ представления больше подходит для разреженных графов, то есть графов у которых количество рёбер гораздо меньше чем количество вершин в квадрате (|E| << |V|²). В данном представлении используется массив Adj содержащий |V| списков. В каждом списке Adj[v] содержатся все вершины u, так что между v и u есть ребро. Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.

Главный недостаток этого способа представления в том, что нет быстрого способа проверить существует ли ребро (u, v).

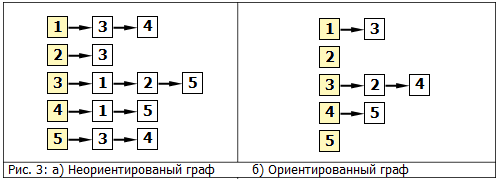
На рис. 3 приведены представления графов из рис. 1 с помощью списков смежности.

⇐ Предыдущая 123 4 Следующая ⇒