Электронные ресурсы: Youtube

Стр 1 из 4Следующая ⇒

Дата: 09 ноября 2020 г.

Номер группы: 121

Дисциплина: ОДУ 11. Информатика

Тема занятия: Решение алгоритмических задач

План изучения нового материала:

Электронные ресурсы: Youtube

1. Граф информационной модели. Использование графов при решении задач. https://www.youtube.com/watch?v=nF9U842EXEw

2. Алгоритм поиска в глубину. https://www.youtube.com/watch?v=Tzc7Z-mOwxY

Граф — это абстрактное представление множества объектов и связей между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Граф может быть ориентированным или неориентированным. В ориентированном графе, связи являются направленными (то есть пары в E являются упорядоченными, например пары (a, b) и (b, a) это две разные связи). В свою очередь в неориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то значит что существует связь (b, a).

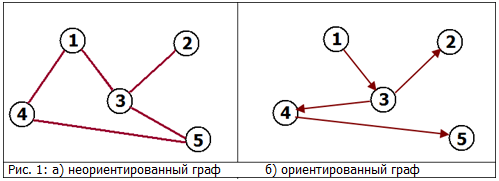
Пример:

Неориентированный граф: Соседство (в жизни). Если (1) сосед (3), то (3) сосед (1). См рис. 1.а
Ориентированный граф: Ссылки. Сайт (1) может ссылаться на сайт (3), но совсем не обязательно (хотя возможно) что сайт (3) ссылается сайт (1). См рис. 1.б

Степень вершины может быть входящая и исходящая (для неориентированных графов входящая степень равна исходящей).

Входящая степень вершины v это количество ребер вида (i,v), то есть количество ребер которые «входят» в v. Исходящая степень вершины v это количество ребер вида (v, i), то есть количество ребер которые «выходят» из v. Это не совсем формальное определение (более формально определение через инцидентность), но оно вполне отражает суть.

Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис 1.б, [(1), (3), (4), (5)].

12 3 4 Следующая ⇒