
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод введения новой переменной.
2. Метод введения новой переменной.
Пусть g(x)=t, тогда уравнение p(g(x))=0 равносильно уравнению p(t)=0.
Пример 3:
Введение новой переменной
Метод введения новой переменной:
1. в уравнении какая-то его часть заменяется другой переменной (a, y, t...)
(прежнее неизвестное одновременно с новым в уравнении быть не может);
2. решается новое уравнение;
3. возвращаются к обозначенному и, используя полученное число (корни), вычисляют требуемое неизвестное.
Пример:
реши уравнение (2x−21)2−5(2x−21)+4=0.
Это уравнение можно решить и без использования новой переменной (раскрываются скобки по формуле разности квадратов и т. д.), но решение будет длинным и с большими числами.
Используем то, что обе скобки равны.
Обозначаем 2x−21=y. Получается простое квадратное уравнение:
y2−5y+4=0 по теореме Виета;y1=4,y2=1.
Возвращаемся к обозначенному:
| 1) 2x−21=4; 2x=25; x=12,5 | 2) 2x−21=1; 2x=22; x=11 |
Ответ: x=12,5; x=11.

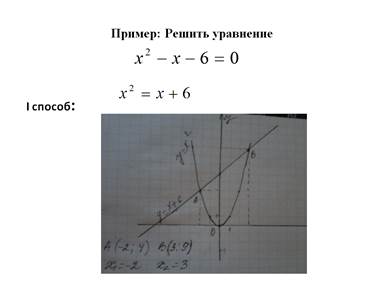
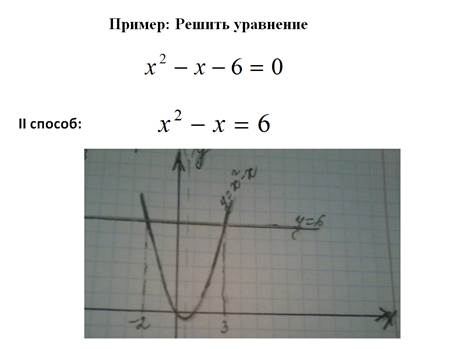


Решите уравнения
| Решить графически Х2-4Х+3=0 |
| Разложите на множители Х2-5Х+4=0 |
| Решить через дискриминант 3Х2-13Х+4=0 |
| 2Х2-9Х-5=0 |
| 9Х2-12Х+4=0 |
| 49Х2-28Х+3=0 |
| 4Х2-Х+1=0 |
Решить любым способом
| 6х(2х+1)=5х+7 |
| 2х(х-8)= -18х-1 |
| 8х(1+2х)= - 1 |
| х(х – 5)=1-4х |
| 4х(х-1) + х(х+2) = 3(2х-1) |
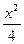 - - 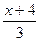 +1=0 +1=0
|
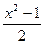 - - 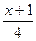 - 3=0 - 3=0
|
| Решить графически (х-2)2=3х-8 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|