Тема занятия «Основные методы решения уравнений»

Тема занятия «Основные методы решения уравнений»

Составьте конспект

Общее решение уравнений

Если к обеим частям уравнения прибавить одно и то же число, то получится уравнение равносильное данному.

и аналогично:

Если из обеих частей уравнения вычесть одно и то же число, то получится уравнение равносильное данному.

Другими словами, корень уравнения не изменится, если к обеим частям данного уравнения прибавить (или вычесть из обеих частей) одно и то же число.

Пример 1. Решить уравнение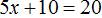

Вычтем из обеих частей уравнения число 10

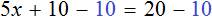
Приведем подобные слагаемые в обеих частях:

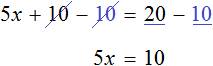
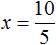
Отсюда .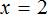

Пример 2. Решить уравнение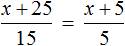

Умнóжим обе части уравнения на 15

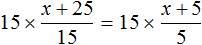
В левой части множители 15 можно сократить на 15, а в правой части множители 15 и 5 можно сократить на 5

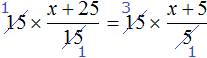
Перепишем то, что у нас осталось:

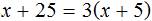
Раскроем скобки в правой части уравнения:

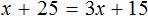
Перенесем слагаемое x из левой части уравнения в правую часть, изменив знак. А слагаемое 15 из правой части уравнения перенесем в левую часть, опять же изменив знак:

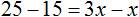
Приведем подобные слагаемые в обеих частях, получим

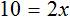
Имеем дело с компонентами умножения. Переменная x является неизвестным сомножителем. Найдём этот известный сомножитель:

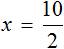
Отсюда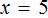

1. Метод разложения на множители.

Уравнение f(x)g(x)h(x)=0 заменить совокупностью уравнений f(x)=0, g(x)=0, h(x)=0. Необходима проверка корней.

Пример 1. Решите уравнение x²+5x=0.
Решение:

		Вынесем за скобку икс.
x(x+5)=0		Разобьем уравнение на два простейших.
x=0 или x+5=0		В первом корень уравнения уже понятен, во втором надо перенести 5 в правую сторону.
x1=0 x2=−5

Ответ: 0; −5.

Пример 2: Решите уравнение x³+4x²−4x−16=0

Решение:

		Перед нами кубическое уравнение. Применим метод группировки: из первой пары слагаемых вынесем x2, а из второй – минус четыре.
Х²(x+4)−4(x+4)=0		Вынесем за скобку x+4x+4.
(x+4)(x²−4)=0		Разложим на множители x2−4x2−4 по формуле сокращенного умножения.
(x+4)(x−2)(x+2)=0		Расщепим уравнения на три.
x+4=0 x−2=0 x+2=0 x1=−4 x2=2 x3=−2

Ответ: −4; 2; −2.

12 Следующая ⇒