Дисперсия дискретной случайной величины

Стр 1 из 2Следующая ⇒

Статистика 02.12.2020 г.

(дисциплина)

Группа : 1011,1010,1009

Преподаватель: Лобасова Т.А.

Тема: Математическое ожидание дискретной случайной величины, свойства.

ЛЕКЦИОНННЫЙ МАТЕРИАЛ

Дисперсия дискретной случайной величины

Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонения её от математического ожидания:

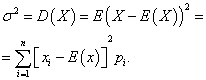
Средним квадратическим отклонением 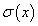случайной величины X называется арифметическое значение квадратного корня её дисперсии:

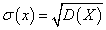Для вычисления дисперсии дискретной случайной величины используют формулу

D(X)= М(Х²)- (М(Х))²

Пример .Вычислить дисперсии случайных величин X и Y, законы распределения которых приведены в таблицах выше.

Решение. Математические ожидания случайных величин X и Y, как было найдено выше, равны нулю. Согласно формуле дисперсии при M(х)=M(y)=0 получаем:

М(X²)=0,01*0,1+0,0001*0,2+0,0001*0,2+0,01*0,1=0,001+0,00002+0,00002+0,001=0,00204

(М(Х))²= 0

D(X)= 0,00204 – 0 = 0,00204

М(У²)= 400*0,3+100*0,1+100*0,1+400*0,3=120+10+10+120=260

(М(У))²=0

D(У)= 260

Таким образом, при одинаковых математических ожиданиях дисперсия случайной величины X очень мала, а случайной величины Y - значительная. Это следствие различия в их распределении.

Пример . Закон распределения случайной величины задан таблицей. Найти D(X)

Х	-1
Р	0,1	0,1	0,2	0,3	0,3

М(Х) = -1*0,1+1*0,2+2*0,3+3*0,3= -0,1+0,2+0,6+0,9=1,6

(М(Х))²= 1,6²= 2,56

М(X²)=1*0,1+1*0,2+4*0,3+9*0,3=0,1+0,2+1,2+2,7=4,2

D(X)= 4,2 – 2,56=1,64

Пример . Закон распределения случайной величины задан таблицей

Х	-2	-1
Р	0,1	0,2	0,1	0,2	0,1	0,3

М(Х)= -2*0,1-1*0,2+1*0,2+2*0,1+3*0,3=0,9

(М(Х))²=0,9²=0,81

М(X²)=3,9

D(X)= 3,9-0,81=3,09

12 Следующая ⇒