
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задание: изучить материал урока, используя конспект и учебник § 10, решить самостоятельную работу № 173 (1,2) и 174 и выполнить домашнюю работу.
Задание: изучить материал урока, используя конспект и учебник § 10, решить самостоятельную работу № 173 (1,2) и 174 и выполнить домашнюю работу.
Урок
Тема: Иррациональные неравенства. Основные приемы их решения.
Цель урока:Научиться решать иррациональные неравенства.
Ход урока
1. Изучение нового материала
Рассмотрим решение простейших неравенств:

Пример: Решить неравенства:
1) 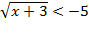
Т. к. корень чётной степени неотрицателен, то решений нет.
2) 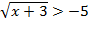
Корень чётной степени неотрицателен, то неравенство выполняется при любом x, допустимом для этого корня. Значит нужно записать ОДЗ для 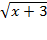 .
.
ОДЗ: 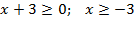
Ответ: 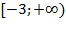
3) 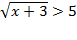
Найдём ОДЗ: 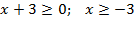
Возведём неравенство в квадрат 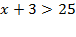 ;
; 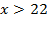 и решим систему неравенств:
и решим систему неравенств:
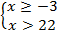 ;
; 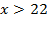
Ответ: 
4) 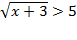
Найдём ОДЗ: 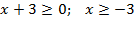
Возведём неравенство в квадрат 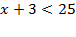 ;
; 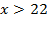 и решим систему неравенств:
и решим систему неравенств:
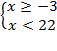 ;
; 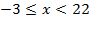
Ответ: 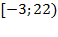
Рассмотрим более сложные примеры. Если в обеих частях неравенства записаны функции.
Существует несколько методов решения иррациональных неравенств. Рассмотрим один из основных.
Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем. Чтобы избежать ошибок при решении иррациональных неравенств, следует рассматривать только те значения переменной, при которых все входящие в неравенство функции определены, т.е. найти ОДЗ этого неравенства, а затем обоснованно осуществлять равносильный переход на всей ОДЗ или ее частях.

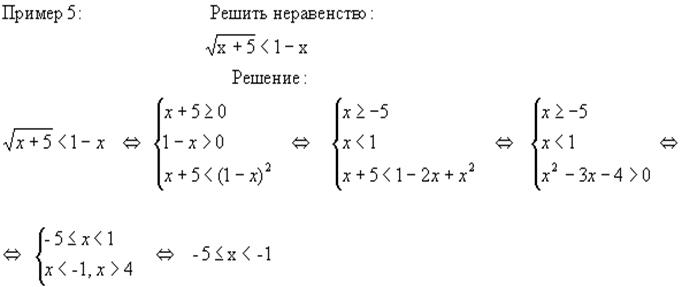 Ответ: [-5;-1).
Ответ: [-5;-1).

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|