Контакты

Случайная статья

Дифференциал функции. dy = f¢(x)dx.. Геометрический смысл дифференциала. Свойства дифференциала

Стр 1 из 2Следующая ⇒

Дифференциал функции

Пусть функция y = f(x) дифференцируема в точке х₀.

Тогда ее приращение можно записать:

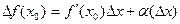, где a(Dх)®0, при Dх®0.

Величина a(Dx) является бесконечно малой, а слагаемое 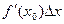является линейной функцией от Dx и составляет главную часть приращения функции.

Дифференциалом функции f(x) в точке х₀ называется линейная относительно Dx функция 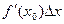, составляющая главную часть приращения функции в точке х₀.

Обозначается df(х₀) или dy.

dy = f¢(x)dx.

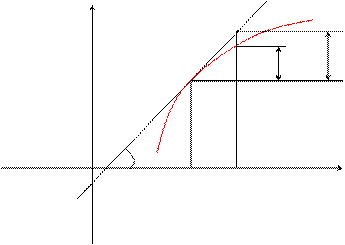
Геометрический смысл дифференциала

y

f(x)

K

dy

M Dy

L

a

x₀ x₀ + Dx x

Из треугольника DMKL: KL = dy = tga×Dx = y¢×Dx

Таким образом, дифференциал функции f(x) в точке х₀ равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.

Свойства дифференциала

Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:

1) d(u ± v) = (u ± v)¢dx = u¢dx ± v¢dx = du ± dv

2) d(uv) = (uv)¢dx = (u¢v + v¢u)dx = vdu + udv

3) d(Cu) = Cdu

4)

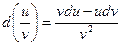
Пример. Найти дифференциал функции .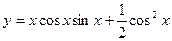

Сначала преобразуем данную функцию: 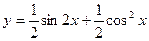, найдем производную

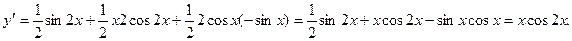
Тогда дифференциал будет равен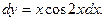

Пример. Найти дифференциал функции .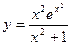

Сначала найдем производную:

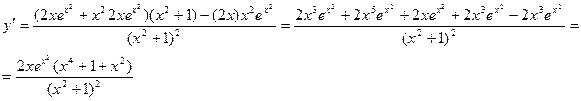
Тогда дифференциал будет равен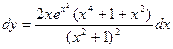

Пример. Найти дифференциал функции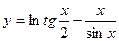

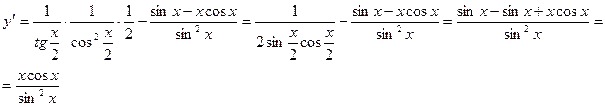
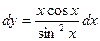
Пример. Найти дифференциал функции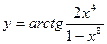

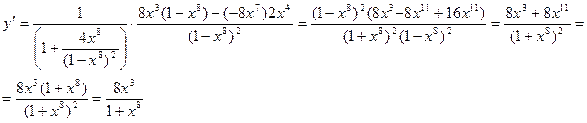
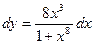
Пример. Найти дифференциал функции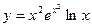

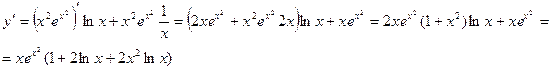
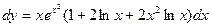
12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.