
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Алгоритм минимизации конечного автомата
4.4. Алгоритм минимизации конечного автомата
Шаг 1: два состояния s и t относим в один класс 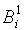 , если для любого входного символа x значение функции выхода s совпадает со значениями функции выхода t. В результате получим r классов:
, если для любого входного символа x значение функции выхода s совпадает со значениями функции выхода t. В результате получим r классов:
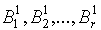 .
.
M
Шаг k: два состояния s и t из одного класса  , полученного на предыдущем шаге, относим в один класс
, полученного на предыдущем шаге, относим в один класс 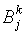 , если для любого значения входного символа значения функций состояний принадлежат одному и тому же классу из предыдущего шага. Если шаг k не изменяет разбиения, то процесс останавливается. Доопределяем функции перехода и выхода и строим таблицу переходов –выходов.
, если для любого значения входного символа значения функций состояний принадлежат одному и тому же классу из предыдущего шага. Если шаг k не изменяет разбиения, то процесс останавливается. Доопределяем функции перехода и выхода и строим таблицу переходов –выходов.
Пример. Минимизировать автомат, заданный таблицей:

Шаг 1: Первое, третье и четвертое состояния отнесем в один класс состояний, а второе, пятое и шестое – в другой:
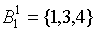 ;
; 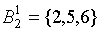
Шаг 2: Выпишем значения функции переходов для состояний из класса 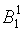 :
:
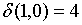 ;
; 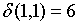 ;
; 
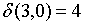 ;
; 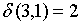 ;
; 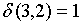
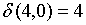 ;
; 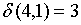 ;
; 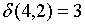
Видно, что 1 и 3-е состояния относим в один класс этого шага  , а четвертое состояние – в другой
, а четвертое состояние – в другой 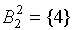 . Проанализировав аналогичным образом значения функции выходов для состояний из класса
. Проанализировав аналогичным образом значения функции выходов для состояний из класса 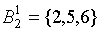 , видим:
, видим:
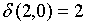 ;
; 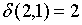 ;
; 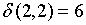
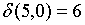 ;
;  ;
; 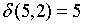
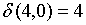 ;
; 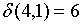 ;
; 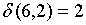 , т.е. все они остаются в одном классе. В результате получим разбиение на классы:
, т.е. все они остаются в одном классе. В результате получим разбиение на классы:
 ;
; 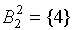 ;
; 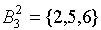
Шаг 3:  ;
; 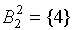 ;
; 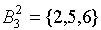 . Дальнейшего разбиения классов не происходит, поэтому процесс останавливается. Класс
. Дальнейшего разбиения классов не происходит, поэтому процесс останавливается. Класс  назовем состоянием
назовем состоянием 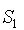 , класс состояний
, класс состояний 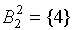 назовем состоянием
назовем состоянием 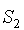 , а класс
, а класс 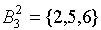 – состоянием
– состоянием 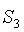 .
.
Построим таблицу переходов–выходов:
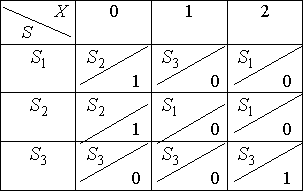
Построенный автомат – минимальный.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|