
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция 4.. Эквивалентные состояния. Минимизация к.д.а
Лекция 4.
4.3. Эквивалентные состояния. Минимизация к.д.а
Определение. Две диаграммы Мура называются изоморфными, если они могут быть превращены одна в другую переобозначением вершин.
Определение. Два автомата называются изоморфными, если их диаграммы Мура изоморфны.
Рассмотрим два автомата 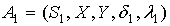 и
и 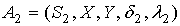 с одинаковыми входным и выходным алфавитами.
с одинаковыми входным и выходным алфавитами.
Определение. Состояния 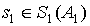 и
и  называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого входного слова х результат работы автомата
называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого входного слова х результат работы автомата  такой же, как и для
такой же, как и для 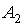 .
.
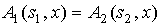
В частном случае, когда  =
= 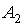 , то речь идет о неотличимых состояниях одного автомата.
, то речь идет о неотличимых состояниях одного автомата.
Определение. Автоматы  и
и 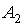 называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого состояния
называются неотличимыми (эквивалентными) тогда и только тогда, когда для любого состояния 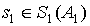 найдется эквивалентное ему состояние
найдется эквивалентное ему состояние  и обратно.
и обратно.
Неотличимые автоматы осуществляют одно и то же отображение входных слов в выходные.
Определение. Автомат А называется приведенным, если в нем нет эквивалентных (неразличимых) состояний.
Число состояний в приведенном автомате минимально. Для любого автомата 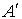 существует эквивалентный ему приведенный автомат А. Процедура нахождения такого автомата называется минимизацией автомата
существует эквивалентный ему приведенный автомат А. Процедура нахождения такого автомата называется минимизацией автомата 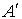 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|