
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Планиметрия. Окружность. Длина окружности С = 2πR. Углы в окружности. Касательные, хорды и секущие. Вписанный четырехугольник. Описанный четырехугольник
Планиметрия. Окружность
Длина окружности С = 2πR
Углы в окружности
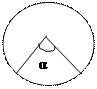 α
α
Вписанный угол равен половине дуги, на которую он опирается
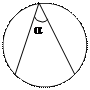 |
2α
Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на диаметр, прямой.
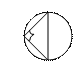

Касательные, хорды и секущие

 В
В
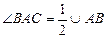
Если хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды
|
|
|

C
AE∙BE = CE∙ED
|

Угол между двумя пересекающимися хордами равен полусумме заключенных между ними дуг
|
А 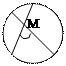 С
С
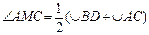
|
|
|
|

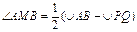
Вписанные правильные многоугольники: 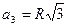 ,
, 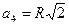 ,
, 

Вписанный четырехугольник
Описанный четырехугольник
В любом вписанном четырехугольнике сумма противоположных углов равна 180°
|
Теорема Птолемея
Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его противоположных сторон
| ||||
| ||||
|
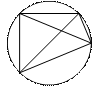
AC∙BD=AD∙BC+ AB∙CD
В любом описанном четырехугольнике суммы противоположных сторон равны
А В
|

С
AD+BC=AB+CD