
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Урок 21. Синус, косинус, тангенс, котангенс
Стр 1 из 2Следующая ⇒
Урок 21. Синус, косинус, тангенс, котангенс
| Цель деятельности учителя | Создать условия для введения понятий синуса, косинуса, тангенса и котангенса для углов от 0° до 180°, выведения основного тригонометрического тождества |
I этап. Мотивация к деятельности
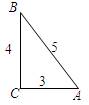 1. Дан треугольник АВС. Чему равен синус угла А? 5. Если cosa =
1. Дан треугольник АВС. Чему равен синус угла А? 5. Если cosa = 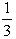 , то чему равен tga?
а)
, то чему равен tga?
а) 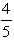 ; б)
; б) 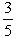 ; в)
; в) 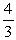 . а)
. а) 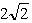 ; б) 8; в)
; б) 8; в) 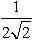 .
2. Чему равен тангенс угла В? 6. В прямоугольном ∆АСВ, sinА =
.
2. Чему равен тангенс угла В? 6. В прямоугольном ∆АСВ, sinА = 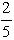 . Найти sinВ.
а)
. Найти sinВ.
а) 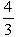 ; б)
; б) 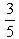 ; в)
; в) 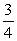 . а)
. а) 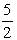 ; б)
; б) 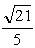 ; в)
; в) 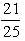 .
3. Чему равен косинус 60°? 7. Упростите выражение: sin30° ∙ cos45° ∙ tg60°.
а)
.
3. Чему равен косинус 60°? 7. Упростите выражение: sin30° ∙ cos45° ∙ tg60°.
а) 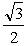 ; б)
; б) 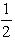 ; в)
; в) 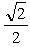 . а)
. а) 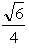 ; б)
; б) 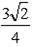 ; в)
; в)  .
4. Если sina =
.
4. Если sina = 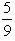 , то чему равен cosa?
а)
, то чему равен cosa?
а) 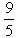 ; б)
; б) 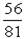 ; в)
; в) 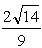 . Мне только буквы из ответов.
. Мне только буквы из ответов.
II этап. Изучение новой темы
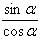 при a ≠ 90°; tg 0° = 0; tg 180° = 0.
5. Вывести основное тригонометрическое тождество sin2a + cos2a = 1, используя рис. 290 в учебнике на с. 248.
6. Составить таблицу:
при a ≠ 90°; tg 0° = 0; tg 180° = 0.
5. Вывести основное тригонометрическое тождество sin2a + cos2a = 1, используя рис. 290 в учебнике на с. 248.
6. Составить таблицу:
| 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | |
| sina | 1/2 | 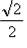
| 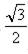
| 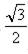
| 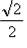
| 1/2 | |||
| cosa | 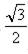
| 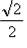
| 1/2 | -1/2 | ___ 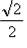
| __ 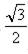
| -1 | ||
| tga | 
| 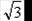
| Не сущ | - 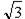
| -1 | 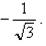
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|