Ответ: 20 кв.см. Решение задач на нахождение элементов конуса. Задача 1. Задача 2. Решение задач на нахождение элементов цилиндра. Задача 1. Задача 2. Решение задач на нахождение элементов шара. Задача 1. Задача 2

⇐ ПредыдущаяСтр 2 из 2

Ответ: 20 кв.см

3. Решение задач на нахождение элементов конуса

Задача 1

Дано: конус, ОР = 15 см, ОВ = r = 8 см.

Найти: РВ.

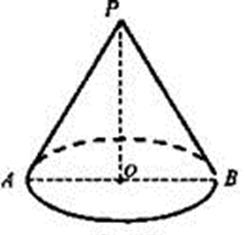
Решение:

Из ΔОРВ по теореме Пифагора;

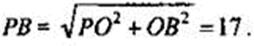
Ответ: 17 см.

Задача 2

Дано: Конус. О₂Р = 8 дм. .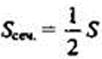

Найти:О₁Р.

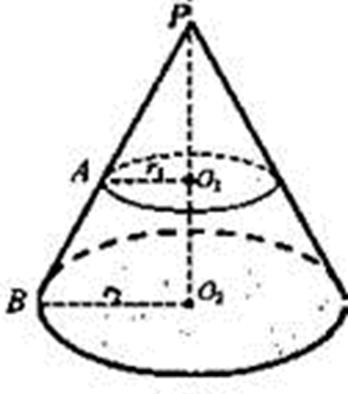
Решение:

Сечение и основание конуса – круги – подобны.

Площади подобных фигур относятся как квадрат коэффициента подобия.

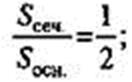
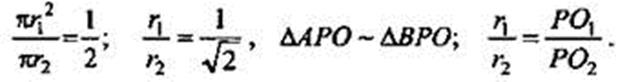
Пусть РО1 = X дм, тогда PO1 - искомый отрезок.

Ответ: 4√2 дм.

4. Решение задач на нахождение элементов цилиндра

Задача 1

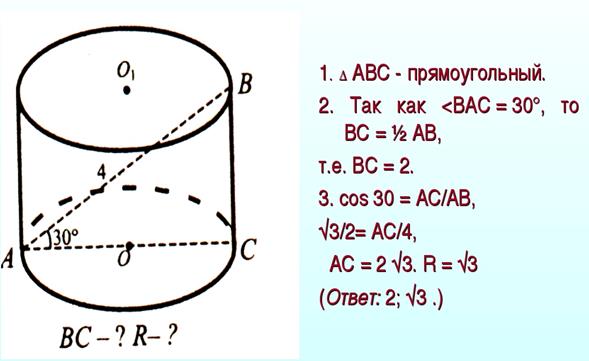
Задача 2

5. Решение задач на нахождение элементов шара

Задача 1

Шар радиуса R = 25 дм пересечен плоскостью, находящейся на расстоянии d = 24 дм от центра шара.

Найти площадь сечения Sсеч. (рис. 1).

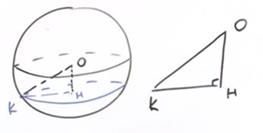Рис. 1. Иллюстрация к задаче 1 и 2

Решение:

1. О – центр шара,

Н – центр круга, который является сечением.

ОН (d) = 24 дм (рис. 1).

Пусть К – произвольная точка на окружности сечения.

Тогда ОК – радиус шара.

2. Рассмотрим треугольник ΔОКН.

По теореме Пифагора:

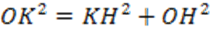тогда радиус плоскости (r) сечения:

;

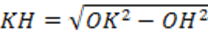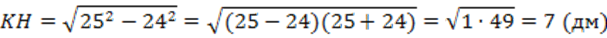
3. Площадь сечения равна:

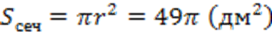, где r – радиус площади сечения.

Ответ: площадь сечения равна .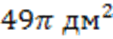

Задача 2

Расстояние от центра шара до секущей его плоскости ОН равно d = 2 см.

Площадь сечения шара Sсеч. = 16 π см².

Найти радиус R данного шара.

Рис. 1. Иллюстрация к задаче 1 и 2

Решение: (См. рис. 1).

1. О – центр шара,

Н – центр круга, который является сечением.

ОН (d) = 2 см (рис. 1).

Пусть К – произвольная точка на окружности сечения.

Тогда ОК – радиус шара, КН – радиус круга сечения.

2. Так как ОК – радиус шара, КН – радиус круга сечения,

Площадь сечения известна из условия:

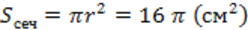Отсюда, радиус сечения (КН) .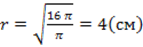

3. Рассмотрим треугольник ΔОКН. По теореме Пифагора:

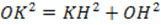, отсюда

радиус шара .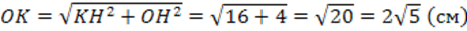

Ответ: радиус шара ОК=R равен 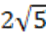см.

⇐ Предыдущая 12