Решение задач на нахождение. элементов пирамиды. Решение задачи на четырехугольную пирамиду. Задача 1. Ответ: 32 кв.см.. Задача 3. Задача 4. Решение задач на нахождение элементов призмы. Задача 1. Задача 2. Задание № 3

1. Решение задач на нахождение

элементов пирамиды

Решение задачи на четырехугольную пирамиду

Задача 1

Основанием пирамиды является квадрат ABCD со стороной 4 см, высота – отрезок .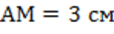

Найти площадь боковой поверхности пирамиды.

Решение:

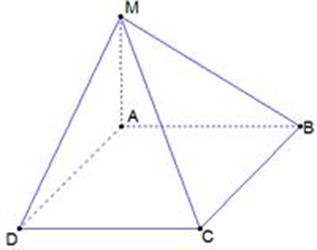
1. Из условия: МА⊥АВС.

2. Прямоугольные треугольники МАВ и MAD равны по двум катетам, отсюда .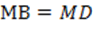

3. Треугольники МCD и МСВ равны по трем сторонам.

Отсюда: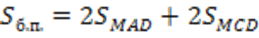

4. AD – проекция прямой MD на плоскость АВС, AD⊥DC⇒MD⊥DC,

отсюда имеем прямоугольный треугольник MDC.

5. В прямоугольном треугольнике MAD найдем по теореме Пифагора гипотенузу:

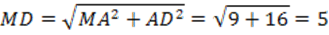6. Найдем площадь рассматриваемого прямоугольного треугольника MAD:

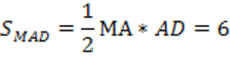
7. Рассмотрим прямоугольный треугольник MDC и найдем его площадь:

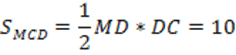
8. Площадь боковой поверхности заданной пирамиды в соответствии с п.3 выражена формулой:

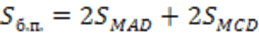В соответствии с п.6 и п.7:

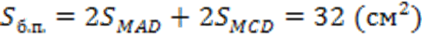Ответ: 32 кв.см.

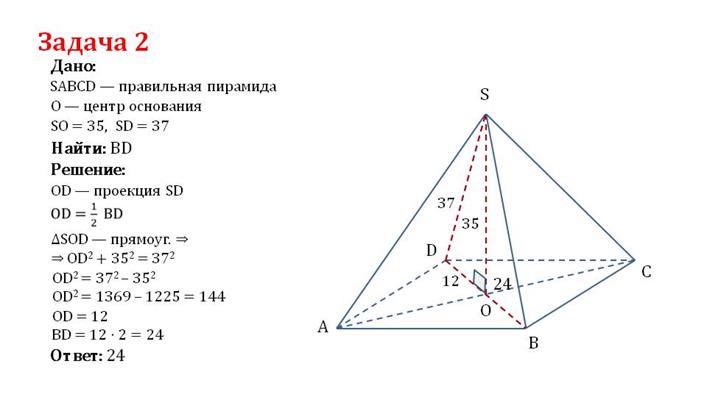
Задача 3

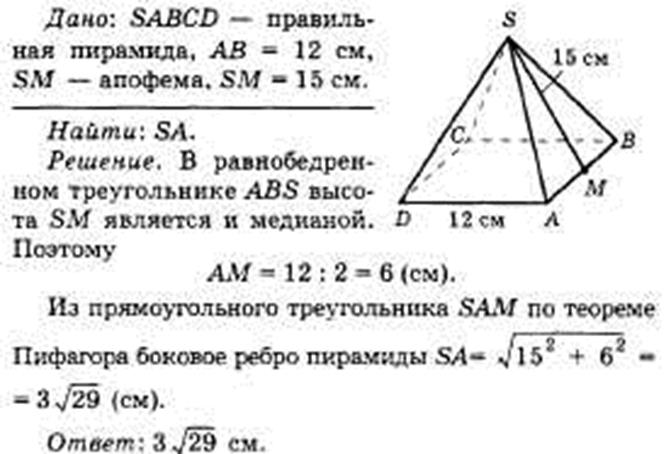
Задача 4

2. Решение задач на нахождение элементов призмы

Задача 1

Задача 2

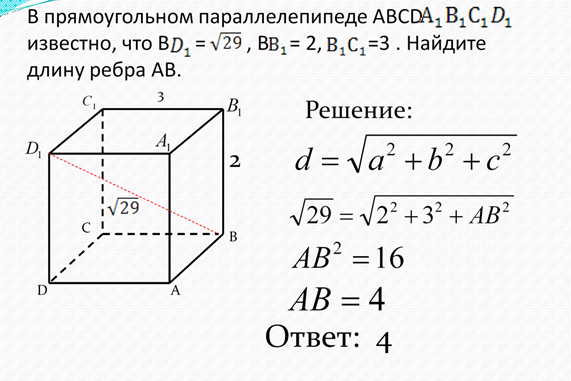
Задание № 3

В правильной треугольной призме ABCA1B1C1 стороны основания равны 4 см, а боковые рёбра равны 10 см.

Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A1B1, A1С1.

Решение:

Рассмотрим следующий рисунок.

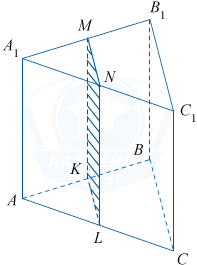
1. Отрезок MN является средней линией треугольника A1B1C1, поэтому

MN = ½ B1C1 = 2.

Аналогично,

KL = ½ BC = 2.

Кроме того, MK = NL = 10.

2. Отсюда следует, что четырёхугольник MNLK является параллелограммом.

Так как MK∥AA, то MK⊥KL и МК⊥АВС и МК⊥KL.

Следовательно, четырёхугольник MNLK является прямоугольником.

3. Так как сечение призмы – это прямоугольник MNLK, то площадь этого прямоугольника:

SMNLK = MN·LK= 10⋅2 = 20.