пересекающиеся;. Теорема. Углы между прямыми

2. пересекающиеся;

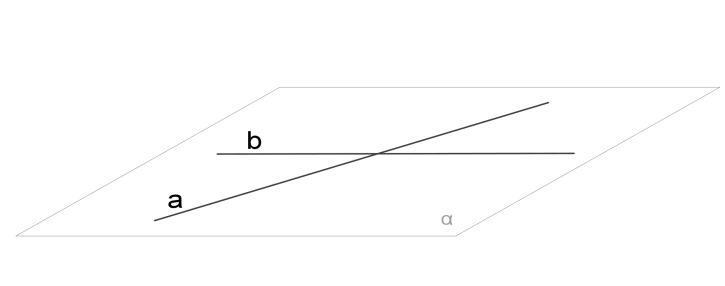
3. скрещивающиеся.

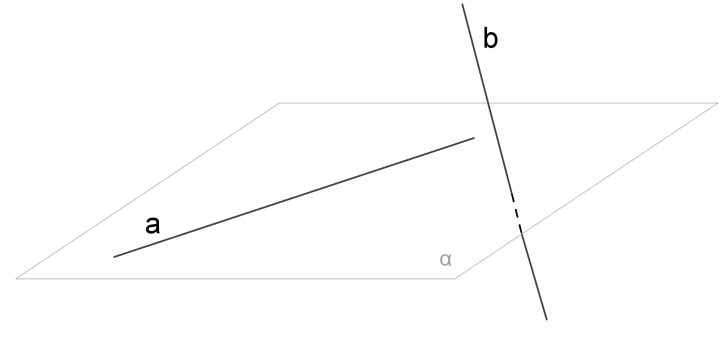
Теорема

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.

1. Через точку D можно провести прямую DE, параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α.
3. Так как прямая AB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Углы между прямыми

1. Если прямые параллельны, то угол между ними — 0⁰.

2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол 90⁰).

3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

Обрати внимание!

Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.

Пример:

дан куб ABCDA₁B₁C₁D₁.

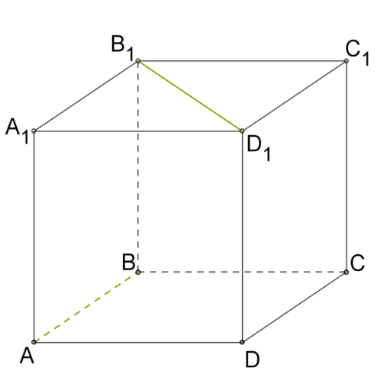
Найти угол между AB и B₁D₁.

Выберем точку B на прямой AB и проведём через B прямую BD параллельно B₁D₁.

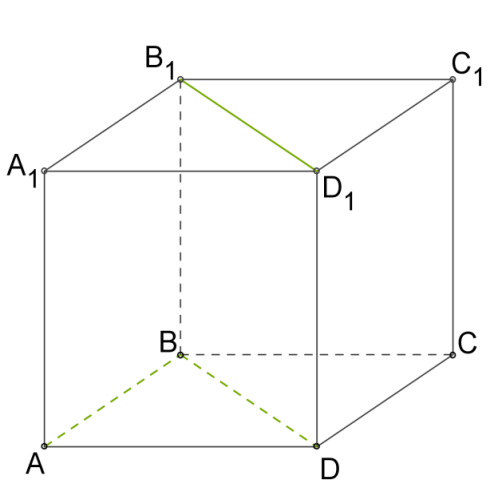
Угол между AB и BD — 45⁰, так как ABCD — квадрат.

Соотвeтственно, угол между AB и B1D1 — тоже 45⁰.

⇐ Предыдущая 12