Лекция 14 Механико - математические модели конструкционных элементов ЛА

Лекция 14 Механико - математические модели конструкционных элементов ЛА

Механико - математическая модель (МММ) может быть определена как совокупность геометрических, механических, физических и других гипотез и соответствующий им математический аппарат.

Рассмотрим наиболее характерные идеализированные МММ конструкционных элементов ЛА, выполненных из изотропного материала, при действии силовых нагрузок. В дальнейшем обратимся и к неизотропным материалам, и к другим типам силовых нагрузок , и к случаям температурных воздействий, приводящимся к термоупругим задачам.

Плоские конструкционные элементы

Наиболее простыми МММ конструкционных элементов являются:

Стержень– это брус, у которого один размер (длина) существенно больше двух других размеров. Описывающее его напряженно-деформированное состояние дифференциальное уравнение имеет вид

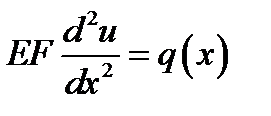где q(x) - произвольно распределенная по длине стержня продольная (осевая) нагрузка, приложенная в центре тяжести (жесткости при несимметричном поперечном сечении) , u(x) - продольное перемещение, EF - жесткость на растяжение-сжатие, E - модуль Юнга, F - площадь поперечного сечения.

Балка– изгибаемый поперечной нагрузкой q(x) брус; w(x) - нормальное (поперечное) перемещение; EJ – изгибная жесткость. J – момент инерции поперечного сечения балки. Дифференциальное уравнение , описывающее деформированное состояние балки, имеет вид

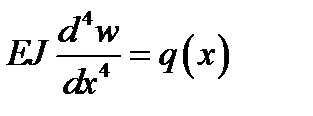
-2-

Стержень и балка – классические задачи сопротивления материалов, решение для которых строится на основе обыкновенных дифференциальных уравнений.

Широкое применение имеют плоские тела - плоские конструкционные элементы в виде тонкостенных элементов двумерных очертаний, нагруженных как в своей плоскости (плоское напряженное состояние), так и изгибаемых нормальной нагрузкой (пластины), для описания деформирования которых необходимо применение дифференциальных уравнений в частных производных.

Так, в случае действия сил в плоскости (плоская задача) проблема определения НДС приводится к следующему дифференциальному уравнению в частных производных:

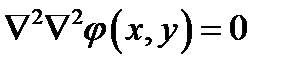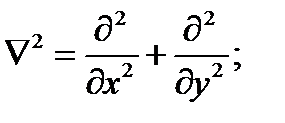
а напряжения связаны с разрешающей функцией 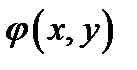, называемой функцией Эри, соотношениями

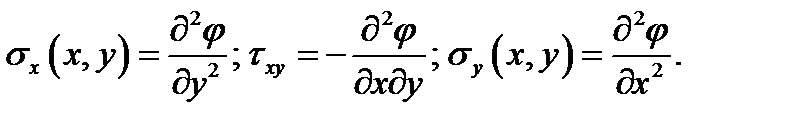
Как и в случае одномерной задачи для стержня, напряжения постоянны по толщине.

При действии на плоское тело прямоугольной формы поперечной нагрузки q(x,y) необходимо решать дифференциальное уравнение в частных производных для изгибаемых пластин

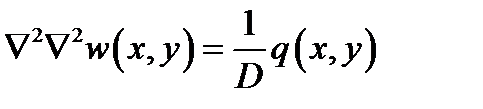
Основные напряжения 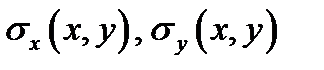при этом поставляют изгибающие моменты

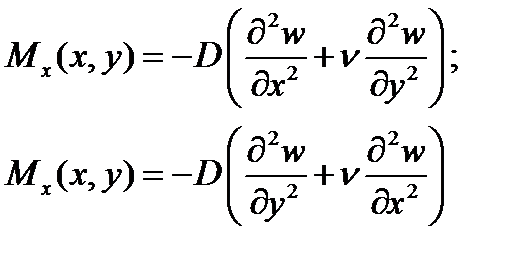
где 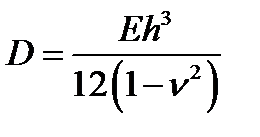-- цилиндрическая жесткость.

Как и в случае одномерной задачи для балки, напряжения здесь линейно изменяются по толщине пластины, принимая нулевое значение на нейтральной плоскости, одинаково отстоящей от лицевых плоскостей пластины.

-3-

Для круглых пластин приведенное выше дифференциальное уравнение и все дифференциальные соотношения легко трансформируется для применения в полярной системе координат.

Оболочки

Случай осесимметричного нормального давления 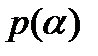( произвольно распределенного в продольном направлении).

Одной из важных и часто встречающихся задач является определение НДС в сферических и конических оболочках, в круговых цилиндрических оболочках при осесимметричном нормальном давлении, произвольно распределенном вдоль образующей.

Получающееся при этом дифференциальное уравнение для цилиндрических оболочек аналогично уравнениям и других типов оболочек (сферических и частично конических) и его решение может служить прекрасной иллюстрацией подхода к реализации такого рода задач.

Итак, в указанном случае имеем основное (разрешающее) дифференциальное уравнение

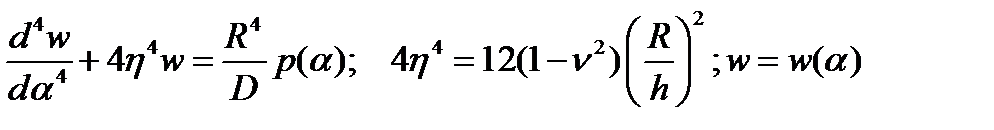записанное относительно нормального перемещения 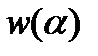в безразмерной системе координат 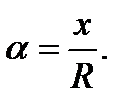Здесь - продольная координата.

Часто , например, у С.П.Тимошенко, это дифференциальное уравнение записывается относительно размерной координаты :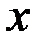

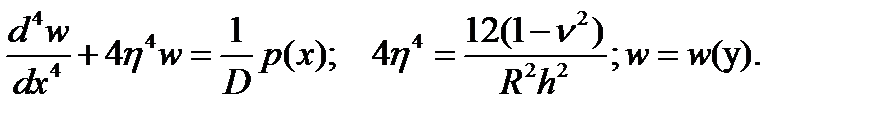
-4-

Случай произвольно распределенного по поверхности оболочки нормального давления .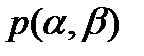

С высокой степенью точности НДС оболочки при любом распределении давления 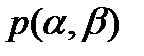может быть определено на основе механико-математической модели, основанной на принятии гипотез Кирхгофа-Лява.

Запишем разрешающее дифференциальное уравнение общей теории круговых цилиндрических оболочек в форме В.З. Власова:

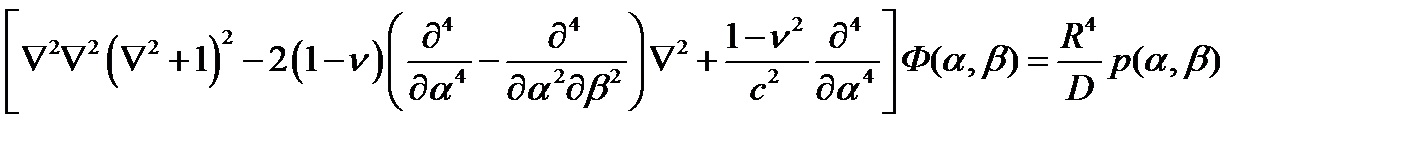
Здесь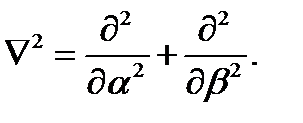

Случай высокой изменяемости нормального давления 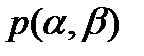в продольном ( α) и окружном (β) направлениях одновременно.

Разрешающее дифференциальное уравнение в данном случае может быть получено путем упрощения только что приведенного уравнения общей теории оболочек по критерию В.В.Новожилова

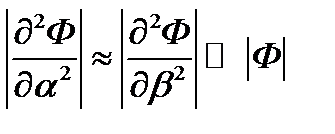
Находим:

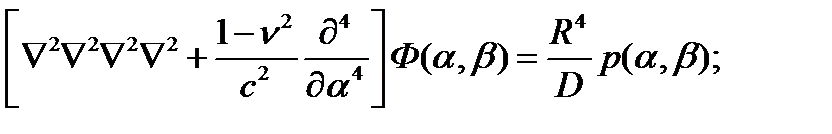
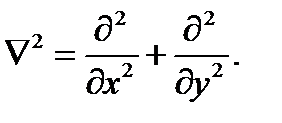
Это известное уравнение теории пологих оболочек В.З.Власова, или дифференциальное уравнение Власова-Доннелла.

-5-

12 Следующая ⇒