Хелпикс

Главная

Контакты

Случайная статья



Треугольник Паскаля

⇐ ПредыдущаяСтр 2 из 2


Треугольник Паскаля

Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:

Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n:

Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.

Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая - для n = 2; третья - для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение:

( a + b )7 , мы можем получить результат моментально, используя таблицу:

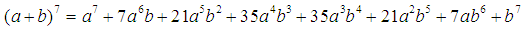
Используя треугольник Паскаля, можно сделать вывод, что, сложив числа в любой строчке треугольника Паскаля, можно получить степень числа 2.

C0n+C1n+...+Cn−1n+Cnn=2n, если n=0;1;2;3...

Пример 1:Разложить бином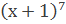

Решение:

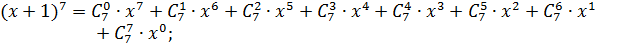
Где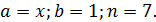

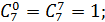
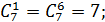
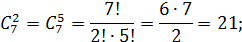
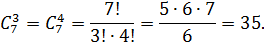
Следовательно,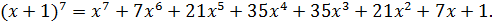

Пример 2: 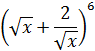Найти: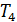

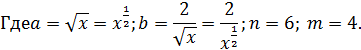
Решение:

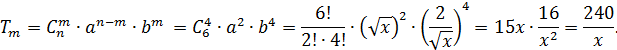
Пример 3:Вычисли средний член разложения (3a+b)6.

Решение:

В разложении 6+1=7 членов, значит, средний член — четвёртый.

 

T4=T3+1=C36(3a)6−3⋅b3=(6⋅5⋅4)/(3⋅2⋅1)⋅27a3b3=540a3b3.

Пример 4:Найдите коэффициент бинома Ньютона для шестого члена разложения выражения .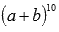

Решение:

В нашем примере n=10, k=6-1=5. Таким образом, мы можем вычислить требуемый биномиальный коэффициент:

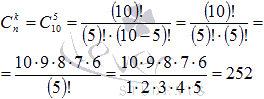
Пример 5:Доказать, что значение выражения 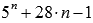, где n – натуральное число, делится на 16 без остатка.

Решение:

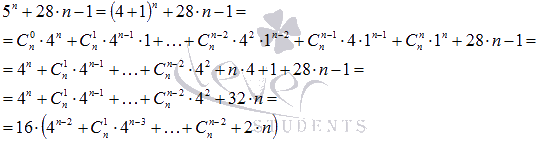
Полученное произведение доказывает делимость исходного выражения на 16.

 


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.