Бином Ньютона. Свойства биномиальных коэффициентов

1. Сделать конспект по теме: Бином Ньютона. Треугольник Паскаля. Разобрать примеры.

2. Посмотреть видео для закрепления:

https://www.youtube.com/watch?v=9NPM-E5q36A - Бином Ньютона. Треугольник Паскаля

https://www.youtube.com/watch?v=Xmy1QpKW5WU – разбор примеров на разложение

Бином Ньютона.

3. Выполнить самостоятельную работу:

- Разложить бином: ;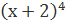

- Разложить выражение 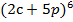по формуле бинома Ньютона.

Бином Ньютона

Формула бинома Ньютона для натуральных n имеет вид

, где 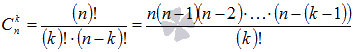- биномиальные коэффициенты, представляющие из себя сочетания из n по k, а все слагаемые — членами бинома.

Эта формула позволяет возвести сумму a+b в любую степень.

К примеру, известная формула сокращенного умножения "квадрат суммы" вида 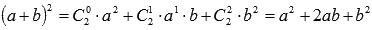есть частный случай бинома Ньютона при n=2.

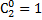
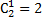
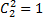
А это разложение бинома Ньютона при n=3: = =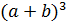

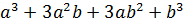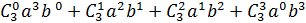
Выражение, которое находится в правой части формулы бинома Ньютона, называют разложением выражения (a+b)ⁿ, а выражение

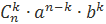называют (k+1)-ым членом разложения, k=0,1,2,…,n.

Свойства биномиальных коэффициентов

Для коэффициентов бинома Ньютона справедливы следующие свойства:

· формула содержит (n+1) ‒ слагаемое;

· показатель степени a ‒ убывает от n до 0; Показатель степени b – возрастает от 0 до n;

· любой член разложения можно найти по формуле:

;

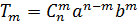· коэффициенты, равноудаленные от начала и конца разложения, равны между собой 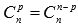, p=0,1,2,…,n;

;

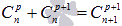· сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома Ньютона:

;

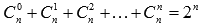· сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.