Содержание заданий, выбор вариантов, порядок выполнения работ

Задача С1

Жёсткая рама, расположенная в вертикальной плоскости (рис. 0 – 9, табл. С1), закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках. В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р=25 кН. 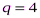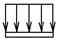На раму действуют пара сил с моментом М=50 кН·м, равномерно распределенная нагрузка интенсивности кН/м, которая действует на участке, указанном для каждого рисунка и сила 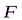, модуль, точка приложения и направление которой указаны в таблице С1; в окончательных расчётах принять a=0,5 м. Направление действия распределённой нагрузки:

горизонтальный участок	вертикальный участок

Определить реакции связей в точках А, В, вызываемые действующими нагрузками.

Указания.Задача С1 – на равновесие тела под действием произвольной плоской системы сил. При её решении учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы 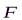удобно разложить её на составляющие 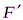и 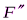, для которых плечи легко определя-ются, и воспользоваться теоремой Вариньона: 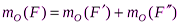. Если в результате решения задачи знак алгебраической величины какой-либо силы оказывается отрицательным, то это означает, что ее направление противоположно первоначально выбранному на чертеже. Необходимо помнить, что по закону действия и противодействия давление данного тела на связь равно по величине и противоположно по направлению реакции связи.

Пример С1. Дано: 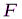=25 кН, =60°, 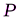=18 кН, 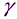=75°, 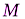=50 кН·м, 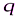=2 кН/м, =30°, 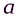=0,5 м (рис. С1).

Определить реакции в точках 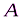, , 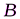вызываемые действующими нагрузками.

Решение. Рассмотрим равновесие рамы. Проведём координатные оси xy и изобразим действующие на раму силовые факторы: силу 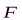, пару сил с моментом М, натяжение троса 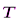(по модулю Т=Р), реакции связей 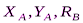(реакцию неподвижной шарнирной опоры А изображаем двумя её составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости); равномерно распределенную нагрузку интенсивности 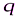, действующую на участке 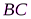, заменяем сосредоточенной силой (по модулю 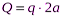=2 кН), которая приложена посередине участка.

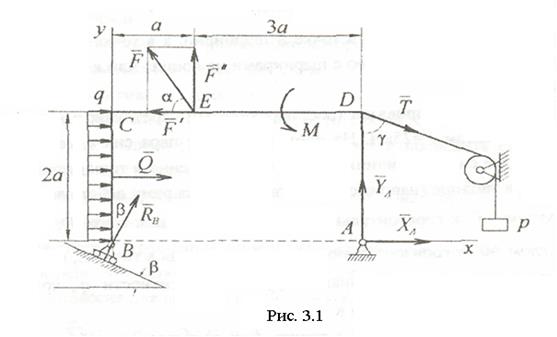
Рис. С1

Для равновесия данной плоской системы сил необходимо и достаточно выполнения трёх уравнений: суммы проекций всех сил на координатные оси x и y, а также сумма их моментов относительно любого центра равны нулю. В третьем уравнении при вычислении момента силы 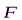относительно точки А воспользуемся теоремой Вариньона, т. е. разложим силу 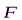на составляющие 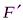, 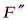( 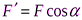, 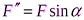) и учтём, что 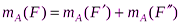. Получим:

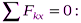
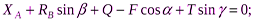
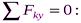
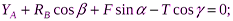
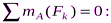
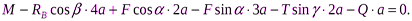
Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.

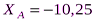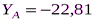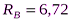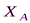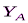Ответ:кН; кН; кН. Знаки указывают, что силы и направлены противоположно показанному на рис. С1.

Выполним проверку решения. Для этого составим еще одно дополнительное уравнение моментов относительно такой точки, чтобы в уравнение вошли найденные реакции 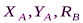. Например, в качестве проверочного можно записать уравнение моментов относительно точки :

.

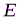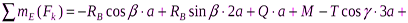
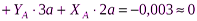При указанных значениях 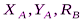последнее уравнение равно нулю с точностью до третьего знака после запятой (погрешность зависит от ошибки, с которой вычислялись искомые реакции), следовательно, задача решена верно.

Таблица С1

Номер условия		0	1	2	3	4	5	6	7	8	9
Сила	модуль кН	10	15	20	25	30	35	40	20	30	10
	точка прилож.	K	H	E	K	H	D	K	H	E	K
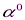
		30	45	60	30	60	30	45	60	30	60
	направ-ление

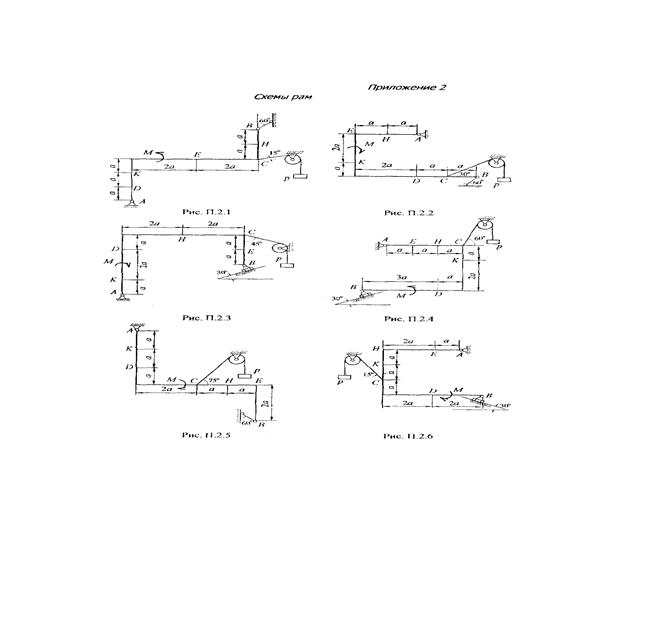Рис. 0 (q на отрезке СЕ) Рис. 1 (q на отрезке KЕ)

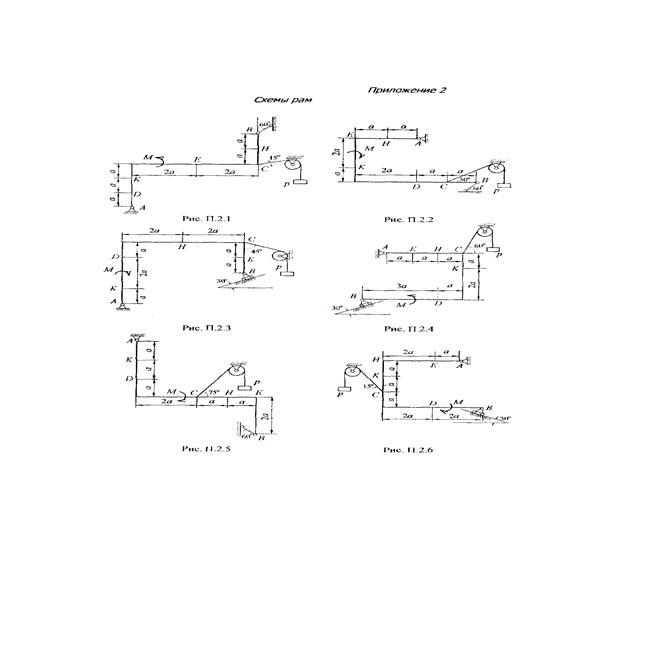Рис. 2 (q на отрезке СН) Рис. 3 (q на отрезке KС)

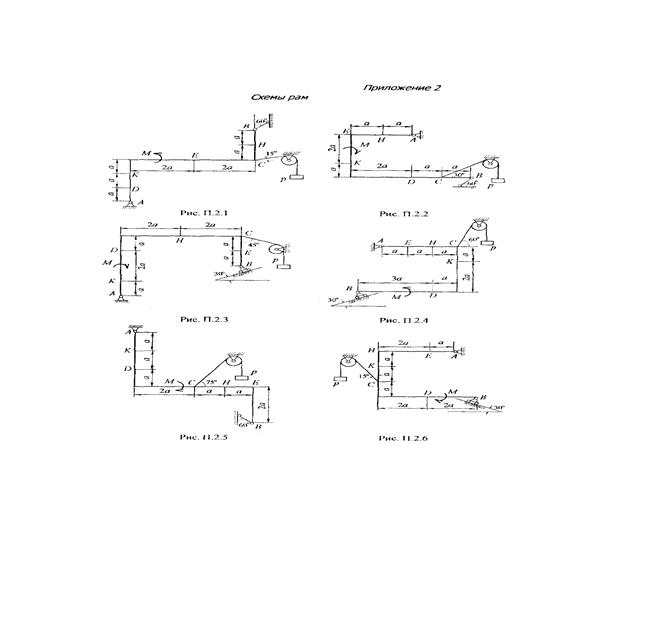
Рис. 4 (q на отрезке НE) Рис. 5 (q на отрезке KН)

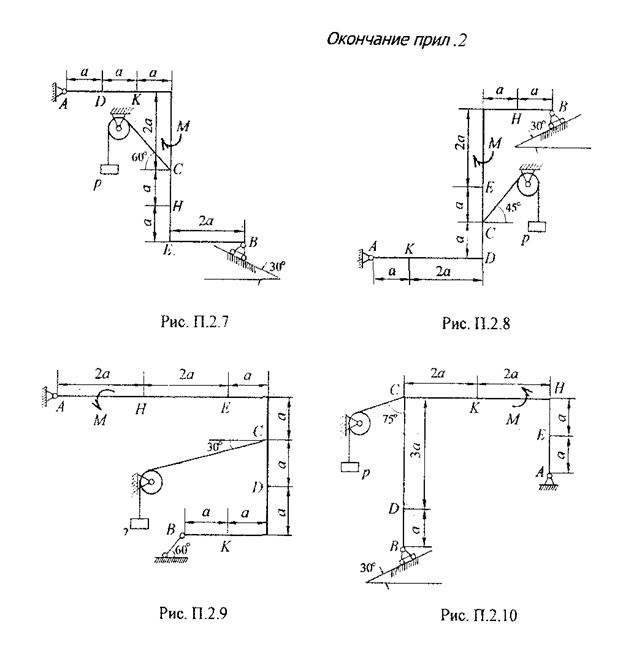
Рис. 6 (q на отрезке KD) Рис. 7 (q на отрезке CD)

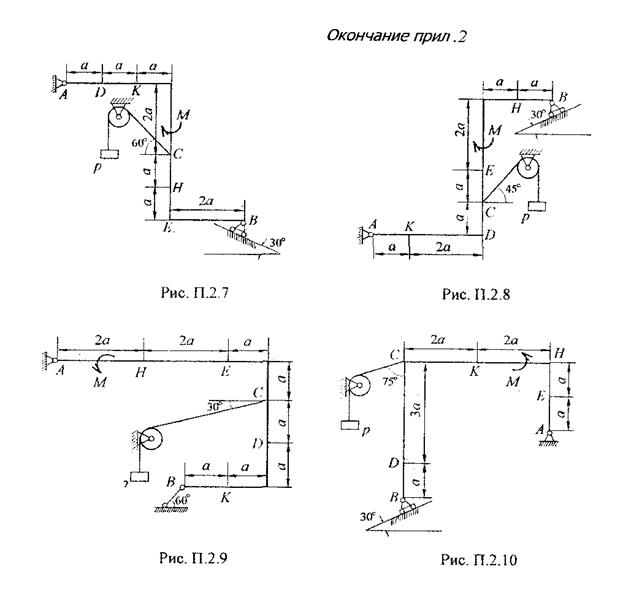
Рис. 8 (q на отрезке HE) Рис. 9 (q на отрезке CD)