МИНОБРНАУКИ РОССИИ. Ухтинский государственный технический университет»

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное

образовательное учреждение высшего образования

«Ухтинский государственный технический университет»

(УГТУ)

Индустриальный институт (СПО)

РАССМОТРЕНО Предметно-цикловой комиссией дисциплин математического и естественного цикла(по программам подготовки специалистов среднего звена) Председатель __________ Е. В. Коваленко «___» ____________ 20___ г.

УТВЕРЖДАЮ Зам. директора по УР Н. Ю. Гаврилина «___»___________ 20__ г.

Банк задач к дифференцированному зачету

по дисциплине математика

2 курс III семестр

очная форма обучения

Специальность

35.02.03 Технология деревообработки

Задачи 01-20Вычислить пределы функций:

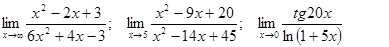
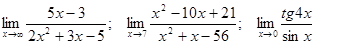
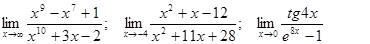
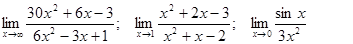
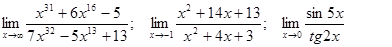
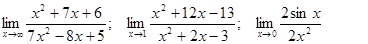
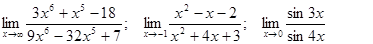
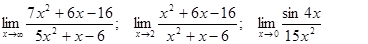
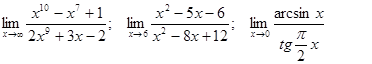
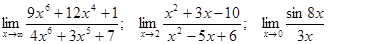
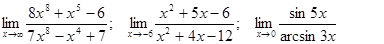
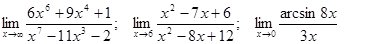
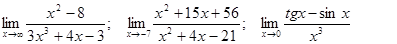
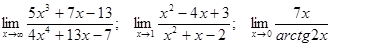
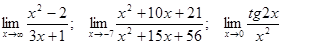
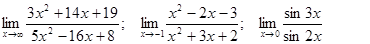
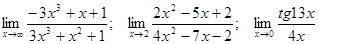
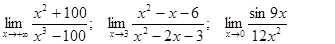
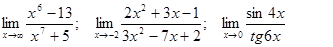
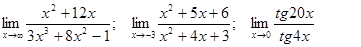
Задачи 21-40Вычислить первую и вторую производные функций:

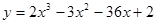
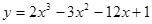
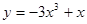
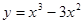
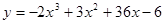
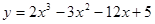
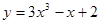
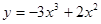
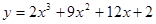
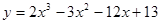
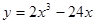
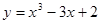
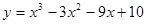
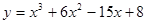
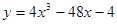
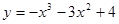
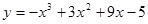
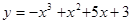
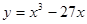
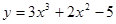
Задачи 41-60Вычислить производные функций:

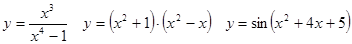
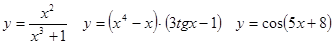
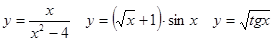
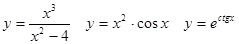
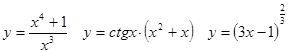
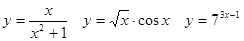
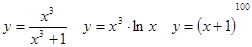
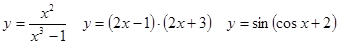
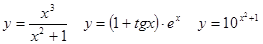
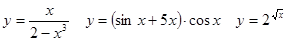
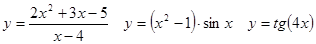
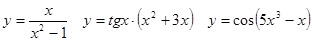
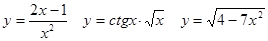
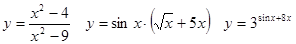
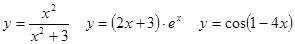
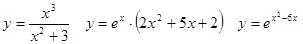
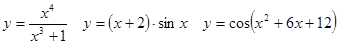
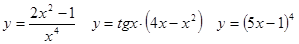
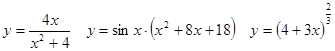
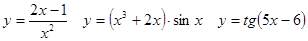
Задачи 61-80 Вычислить неопределённые интегралы:

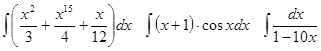
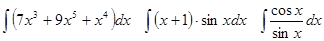
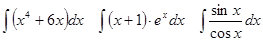
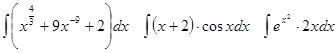
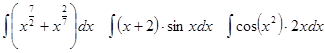
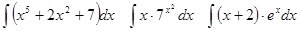
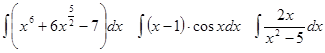
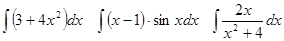
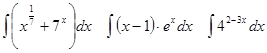
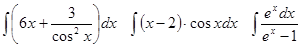
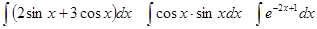
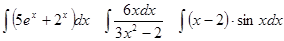
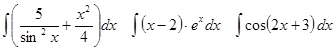
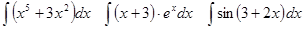
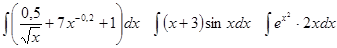
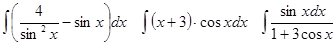
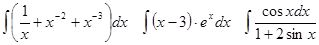
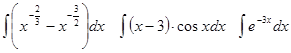
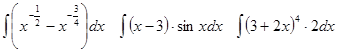
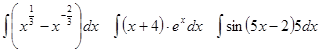
Задачи 81-100 Найти общее решение обыкновенных дифференциальных уравнений 1 порядка:

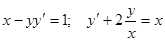
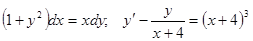
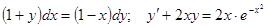
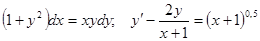
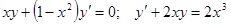
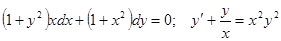
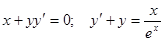
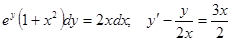
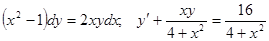
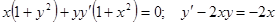
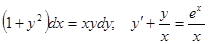
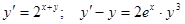
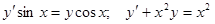
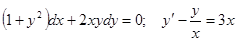
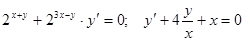
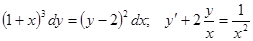
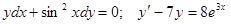
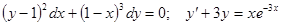
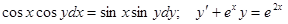
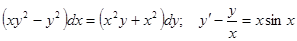
Задачи 101-120 Найти общее решение линейного однородного дифференциального уравнения 2 порядка:

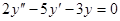
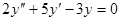
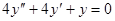
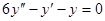
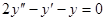
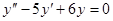
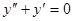
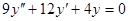
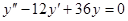
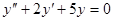
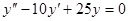
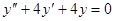
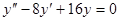
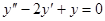
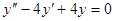
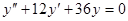
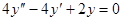
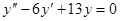
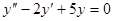
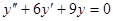
Задачи 121-140 По признаку Даламбера определить сходится ли числовой знакоположительный ряд:

12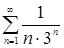1. 131.

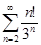
12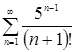2. 132.

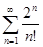
12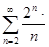3. 133.

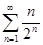
12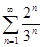4. 134.

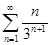
12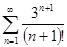5. 135.

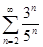
12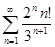6. 136.

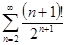
12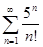7. 137.

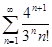
12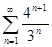8. 138.

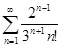
129. 139.

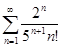
13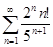0. 140.

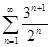
Задачи 141-160 Для треугольника PQL заданы координаты всех его вершин.

Необходимо найти уравнения сторон PQ и QL, длину стороны PQ.

№ вершины
P	(-1;0)	(6;0)	(2;2)	(6;-1)	(-2;-7)	(-2;3)	(1;-4)	(-5;4)	(0;-1)	(-3;-1)
Q	(12;-3)	(0;4)	(1;11)	(9;5)	(6;-11)	(10;-7)	(3;2)	(5;-2)	(8;3)	(-3;5)
L	(5;3)	(-9;-4)	(6;6)	(3;12)	(8;3)	(4;5)	(-4;8)	(3;12)	(-9;2)	(9;-4)

№ вершины
P	(-3;-2)	(1;7)	(9;2)	(1;-1)	(1;-5)	(-2;-8)	(-5;5)	(2;-1)	(1;-3)	(-1;3)
Q	(3;1)	(-4;3)	(3;6)	(-1;3)	(5;1)	(1;2)	(0;-1)	(-1;-7)	(5;5)	(-8;1)
L	(-4;5)	(-1;6)	(-4;4)	(11;-1)	(0;7)	(-5;1)	(5;10)	(5;-14)	(-9;6)	(2;-1)

Задачи 161-170 Известны координаты точек L и M, и радиус окружности R, центр которой находится в начале координат.

точки №	L	M	R

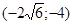
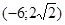
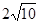
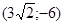
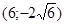
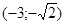
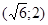
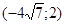
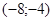
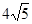
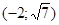
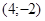
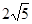
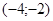
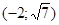
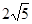
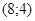
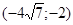
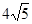
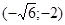
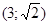
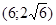
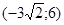
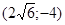
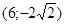
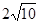
Необходимо:

1) Составить каноническое уравнение эллипса, проходящего через данные точки L и M;

2) Найти полуоси, фокусы и эксцентриситет этого эллипса;

3) Найти все точки пересечения эллипса с данной окружностью;

4) Построить эллипс и окружность.

171– 180.Известны координаты точек L и M.

точки №	L	M	точки №	L	M

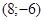
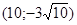
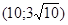
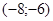
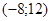
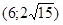
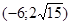
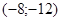
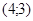
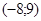
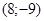
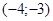
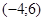
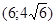
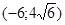
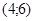
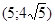
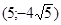
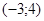
Необходимо:

1) Составить каноническое уравнение гиперболы, проходящей через данные точки L и M, если фокусы гиперболы расположены на оси абсцисс;

2) Найти полуоси, фокусы, эксцентриситет гиперболы;

3) Найти уравнения асимптот гиперболы;

4) Найти все точки пересечения гиперболы с окружностью, центр которой находится в начале координат, а сама окружность проходит через фокусы гиперболы;

Построить гиперболу, её асимптоты, и окружность.

12 Следующая ⇒