
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант 3. Задача 1. Задача 2. Вариант 4. Задача 1. Задача 2. Вариант 5. Задача 1. Задача 2. Вариант 6. Задача 1. Задача 2. Вариант 7. Задача 1. Задача 2. Вариант 8. Задача 1. Задача 2. Вариант 9. Задача 1. Задача 2. Вариант 10. Задача 1. Задача 2. Образе
Вариант 3
Задача 1
Рассчитать показатели риска активов А и В, если известна следующая информация:
Вероятностные распределения доходности акций А и В:
| Спрос | Вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -55 | |
Какой актив является наиболее предпочтительным для инвестирования?
Задача 2
На основе данных задачи 1 рассчитать показатели риска портфеля №1, состоящего из 40% акций А и 60% акций В, и портфеля №2, состоящего из 30% актива А и 70% актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности?
Вариант 4
Задача 1
Рассчитать показатели риска активов А и В, если известна следующая информация:
Вероятностные распределения доходности акций А и В:
| Спрос | Вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -75 | |
Какой актив является наиболее предпочтительным для инвестирования?
Задача 2
На основе данных задачи 1 рассчитать показатели риска портфеля №1, состоящего из 35% акций А и 65% акций В, и портфеля №2, состоящего из 30% актива А и 70% актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности?
Вариант 5
Задача 1
Рассчитать показатели риска активов А и В, если известна следующая информация:
Вероятностные распределения доходности акций А и В:
| Спрос | Вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -45 | |
Какой актив является наиболее предпочтительным для инвестирования?
Задача 2
На основе данных задачи 1 рассчитать показатели риска портфеля №1, состоящего из 40% акций А и 60% акций В, и портфеля №2, состоящего из 30% актива А и 70% актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности?
Вариант 6
Задача 1
Рассчитать показатели риска активов А и В, если известна следующая информация:
Вероятностные распределения доходности акций А и В:
| Спрос | Вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -84 | |
Какой актив является наиболее предпочтительным для инвестирования?
Задача 2
На основе данных задачи 1 рассчитать показатели риска портфеля №1, состоящего из 35% акций А и 65% акций В, и портфеля №2, состоящего из 30% актива А и 70% актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности?
Вариант 7
Задача 1
Рассчитать показатели риска активов А и В, если известна следующая информация:
Вероятностные распределения доходности акций А и В:
| Спрос | Вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -29 | |
Какой актив является наиболее предпочтительным для инвестирования?
Задача 2
На основе данных задачи 1 рассчитать показатели риска портфеля №1, состоящего из 40% акций А и 60% акций В, и портфеля №2, состоящего из 30% актива А и 70% актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности?
Вариант 8
Задача 1
Рассчитать показатели риска активов А и В, если известна следующая информация:
Вероятностные распределения доходности акций А и В:
| Спрос | Вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -59 | |
Какой актив является наиболее предпочтительным для инвестирования?
Задача 2
На основе данных задачи 1 рассчитать показатели риска портфеля №1, состоящего из 35% акций А и 65% акций В, и портфеля №2, состоящего из 30% актива А и 70% актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности?
Вариант 9
Задача 1
Рассчитать показатели риска активов А и В, если известна следующая информация:
Вероятностные распределения доходности акций А и В:
| Спрос | Вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -60 | |
Какой актив является наиболее предпочтительным для инвестирования?
Задача 2
На основе данных задачи 1 рассчитать показатели риска портфеля №1, состоящего из 40% акций А и 60% акций В, и портфеля №2, состоящего из 30% актива А и 70% актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности?
Вариант 10
Задача 1
Рассчитать показатели риска активов А и В, если известна следующая информация:
Вероятностные распределения доходности акций А и В:
| Спрос | Вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -90 | |
Какой актив является наиболее предпочтительным для инвестирования?
Задача 2
На основе данных задачи 1 рассчитать показатели риска портфеля №1, состоящего из 35% акций А и 65% акций В, и портфеля №2, состоящего из 30% актива А и 70% актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности?
Образец решения
Задача 1
Рассчитать показатели риска активов А и В, если известна следующая информация:
Вероятностные распределения доходности акций А и В:
| Спрос | Вероятность | Доходность акций, % | |
| А | В | ||
| Высокий | 0,3 | ||
| Средний | 0,4 | ||
| Низкий | 0,3 | -70 | |
Какой актив является наиболее предпочтительным для инвестирования?
Решение:
1) на первом этапе рассчитываем с помощью ожидаемую доходность активов А и В.
Ожидаемая доходность ( 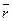 )по каждому активу является одной из важнейших характеристик эффективности инвестиций. Для ее расчета используется следующая формула:
)по каждому активу является одной из важнейших характеристик эффективности инвестиций. Для ее расчета используется следующая формула:
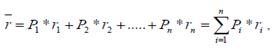
где 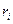 – один из возможных исходов;
– один из возможных исходов;
Pi – вероятность наступления исхода i;
i – общее число возможных исходов.
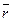 А = 0,3*100+0,4*15-70*0,3 = 15%;
А = 0,3*100+0,4*15-70*0,3 = 15%;
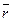 В = 0,3*20+0,4*15+10*0,3 = 15%.
В = 0,3*20+0,4*15+10*0,3 = 15%.
2) на втором этапе рассчитываем стандартное отклонение актива А и В.
Стандартное отклонение ( 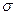 )или корень из дисперсии рассчитывается по следующей формуле:
)или корень из дисперсии рассчитывается по следующей формуле:
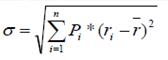 .
.
Данная характеристика является наиболее распространенной для численной оценки риска. Очень часто стандартное отклонение и называют риском (почти всегда при финансовых инвестициях). Отметим, что данный показатель позволяет оценить отклонения величин доходности от ожидаемого значения. Соответственно, чем меньше разброс значений доходности при различных состояниях экономики, тем меньшим уровнем риска будет характеризоваться данный актив. Необходимо понимать, что использование стандартного отклонения или дисперсии как меры риска предполагает нормальное распределение доходности, иными словами, значения доходностей актива при разных состояниях экономики должны быть симметричны относительно ожидаемой доходности. В противном случае использование данных показателей для оценки риска является нецелесообразным, так как даст неверный результат.
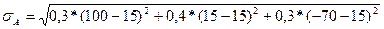 = 65,84;
= 65,84;
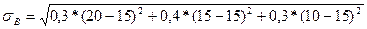 = 3,87.
= 3,87.
Риск акций В ниже риска акций А т.к. 65,84 > 3,87.
3) Далее рассчитываем коэффициент вариации активов А и В.
Известно, что уровень риска и величина доходности в большинстве случаев находятся в прямой зависимости, т. е. увеличение доходности возможно при соответствующем увеличений риска активы, и наоборот. Но мера риска является величиной условной и относительной, поэтому может так оказаться, что некоторые проекты обладают одинаковым риском, рассчитанным по одному из двух предложенных методов. В этом случае для оценки риска используется показатель коэффициента вариаций (Var), который рассчитывается как отношение стандартного отклонения к ожидаемой доходности:
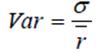 .
.
Из нескольких альтернативных активов, предпочтение отдается тому активу, который имеет наименьший коэффициент вариации, т.е. имеет наименьший уровень риска на единицу доходности.
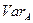 = 65,84/15 = 4,39;
= 65,84/15 = 4,39;
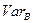 = 3,87/15 = 0,258.
= 3,87/15 = 0,258.
Вывод по задаче: предпочтительней является актив В т.к. коэффициент вариации принимает минимальное значение.
Задача 2
На основе данных задачи 1 рассчитать показатели риска портфеля №1, состоящего из 50% акций А и 50% акций В, и портфеля №2, состоящего из 30% актива А и 70% актива В. Какой портфель является наиболее предпочтительнее с точки зрения оптимизации риска и доходности?
Решение:
1) На первом этапе рассчитываем ожидаемую доходность портфелей активов № 1 и 2:
Ожидаемая доходность портфеля ценных бумаг ( 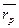 ) – это просто средневзвешенное значение ожидаемых доходностей отдельных активов, входящих в портфель; при этом их веса – это доли общей суммы инвестиций в портфель (часть всего портфеля) вложенные в соответствующие активы:
) – это просто средневзвешенное значение ожидаемых доходностей отдельных активов, входящих в портфель; при этом их веса – это доли общей суммы инвестиций в портфель (часть всего портфеля) вложенные в соответствующие активы:
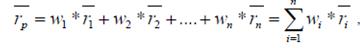
где 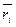 – ожидаемая доходность отдельного актива;
– ожидаемая доходность отдельного актива;
wi – доля этих активов в портфеле из n акций.
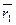 = 0,5*15+0,5*15=15%;
= 0,5*15+0,5*15=15%;
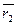 = 0,3*15+0,7*15=15%.
= 0,3*15+0,7*15=15%.
2) На втором этапе рассчитываем стандартное отклонение портфелей №1 и 2. Для этого необходимо рассчитать ковариацию, корреляцию.
Ковариация (covariance) – это показатель, учитывающий как изменчивость (волатилъностъ) доходности акций или портфелей, так и тенденцию их доходности к росту или снижению по мере того, как растет или снижается доходность других акций или портфелей. Формула определяет ковариацию доходности активов А и В (Cov(AB)):
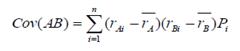 ,
,
где 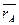 ,
, 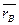 – ожидаемая доходность активов А и В;
– ожидаемая доходность активов А и В;
rAi, rBi – доходность активов А и В в i состоянии;
Pi – вероятность наступления i состояния.
Величину ковариации обычно оказывается довольно сложно интерпретировать, и поэтому для измерения степени совместного изменения переменных чаще используется другой показатель – коэффициент корреляции (correlation coefficient).Коэффициент корреляции стандартизует ковариантность при делении на произведение, что облегчает сравнения при применении аналогичной шкалы. Коэффициент корреляции (rAB) вычисляется для переменных следующим образом:
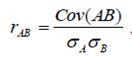
где 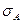 ,
, 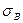 – стандартное отклонение А и В.
– стандартное отклонение А и В.
В целом, используя данные корреляции, можно сделать выводы:
1) чем меньше коэффициент корреляции акций в портфеле, тем меньше риск портфеля, поэтому при формировании портфеля следует включить в него акции, имеющие наименьшую корреляцию;
2) если коэффициент корреляции акций в портфеле +1, то риск портфеля усредняется;
3) если коэффициент корреляции акций в портфеле меньше +1, то риск портфеля уменьшается;
4) если коэффициент корреляции акций в портфеле –1, то можно получить портфель без риска.
Cov(AB)=(100-15)(20-15)*0,3+(15-15)(15-15)*0,4+(-70-15)(10-5)*0.3=255
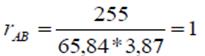
Значение коэффициента корреляции говорит о том, что связь между доходностями прямая.
Для определения риска портфеля, состоящего из двух активов, используют стандартное отклонение портфеля ( 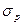 ), которое рассчитывают по следующей формуле:
), которое рассчитывают по следующей формуле:
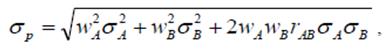
где 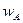 – доля средств портфеля, инвестированная в актив А;
– доля средств портфеля, инвестированная в актив А;
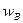 – доля средств портфеля, инвестированная в актив В.
– доля средств портфеля, инвестированная в актив В.
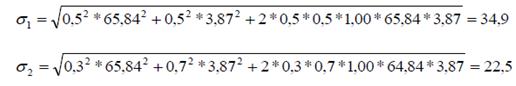
Первый портфель обладает более высоким риском по сравнению со вторым. Это происходит в результате того, что в первом портфеле удельный вес высокорискового актива «А» составляет 50%, в портфеле №2 - 30%
3) Далее рассчитаем коэффициент вариации:
Коэффициента вариаций портфеля (VarAB) рассчитывается как отношение стандартного отклонения портфеля к ожидаемой доходности портфеля:
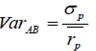 .
.
Из нескольких альтернативных портфелей активов, предпочтение отдается тому портфелю, который имеет наименьший коэффициент вариации, т.е. имеет наименьший уровень риска на единицу доходности.
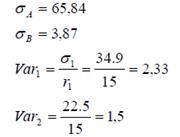
Вывод:Наиболее предпочтительным является второй портфель, т.к. он имеет наименьший коэффициент вариации.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|