
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Преобразование выражений, содержащих степени и корни.
Преобразование выражений, содержащих степени и корни.
Арифметический корень n-й степени и его свойства.
Арифметическим корнем натуральной степениn≥2из неотрицательного числа aназывается неотрицательное число,n-ястепень которого равнаa.
Арифметический корень n-ой степени из числа a обозначается так: 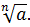
Число aназывается подкоренным выражением. Если n=2, то вместо 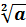 пишут
пишут 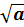 .
.
Арифметический корень второй степени называют такжеквадратным корнем,а корень третьей степени– кубическим корнем.
Чтобы, используя определение, доказать, что корень n-й степени 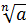 (a≥0)равенb (
(a≥0)равенb ( 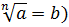 ,нужно показать, что: 1). b
,нужно показать, что: 1). b 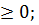 2).
2). 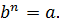
Например, 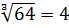 , так как 4
, так как 4 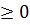 и
и 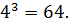
Из определения арифметического корня следует, что если a 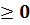 , то
, то 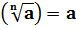 , а также
, а также 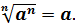
Например, 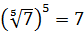 ,
, 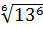 =13.
=13.
Действие, посредством которого отыскивается корень n-ой степени, называется извлечением корня n-ой степени. Это действие является обратным действием возведения в n-ю степень.
Решите уравнение: 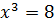 ,
, 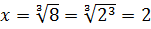 .
.
Решите уравнение: 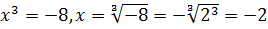 . Число -2 называют кубическим корнем из -8.
. Число -2 называют кубическим корнем из -8.
Задание 1. Вычислить 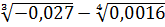 -
- 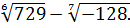
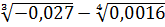 -
- 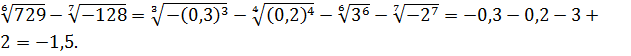
Свойства арифметического корня n-ой степени.
Арифметический корень n-ой степени обладает следующими свойствами: если a 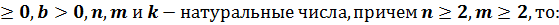
1. 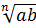 =
= 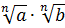 .
.
2. 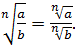
3. 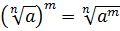 .
.
4. 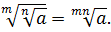
5. 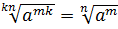 .
.
6. 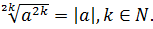
Примеры применения свойств арифметического корня:
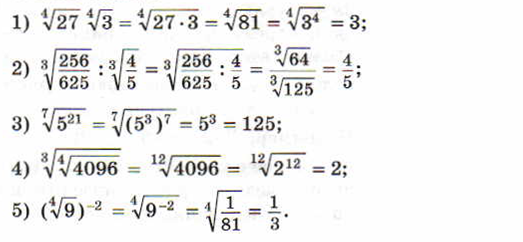
Задание 2. Вычислить: 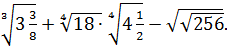
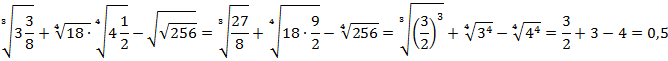
Задание 3. Упростить выражение 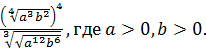
Используя свойства арифметического корня, получаем:
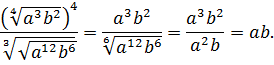
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|