Амплитудная модуляция

1. Амплитудная модуляция

Уравнение АМ колебания имеет вид: 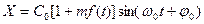, (1) в котором m-коэффициент модуляции, определяемый отношением отклонения амплитуды ВЧ колебаний к их среднему значению m= 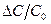, f(t) – низкочастотная модулирующая функция. Если эта функция гармоническая 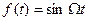, то уравнение АМ колебания примет вид 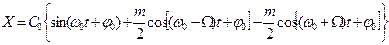(2) Из уравнения видно, что в спектре АМ колебания при модуляции одним тоном имеется три составляющих: с частотой несущего колебания 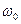и два боковых колебания с суммарной 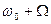и разностной 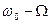частотами, соответственно.

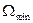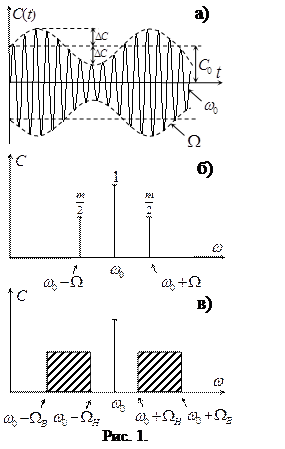
Если модулирующая функция имеет спектр, ограниченный частотами снизу и 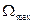сверху, то в спектре АМ колебания возникнут две боковых полосы со спектральной шириной, равной ширине спектра модулирующей функции. Вид временной функции АМ колебания, а также соответствующие спектры иллюстрируются на рис.1(а, б, в).

Иногда применяется АМ колебание балансного типа (с подавленной несущей), описываемое уравнением 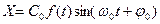, (3) которое при гармонической функции 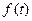примет вид : 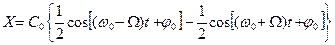(4) КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Сформулировать понятие спектра сигнала и отметить особенности спектров периодических сигналов.

2. Дать определение ширина спектра сигнала и указать на ее связь с параметрами сигнала (например, прямоугольного).

3. Как меняется форма прямоугольного сигнала, синтезируемого из разного числа гармоник?

4. Какой вид имеет спектр амплитудно-модулированного (АМ) колебания (при модуляции одним тоном) и как он меняется при изменении амплитуды и частоты модулирующего сигнала?

5. Каков спектр АМ сигнала при модуляции несущей частоты полосой низкочастотных сигналов?

Особенностью данной работы является компьютерный расчет спектров, например с помощью программы “Fourier Scope”.

ЗАДАНИЕ К РАБОТЕ.

А) Экспериментально снять спектры периодической последовательности импульсов прямоугольной формы при скважностях Q=2; 3; 5; 10. Около каждой спектральной линии (внизу) проставить карандашом ее порядковый номер(включая и нулевой). Для распечатки спектров достаточно выделить первые 15-20 линий.

Б) Снять и построить спектральные диаграммы амплитудно-модулированных колебаний при вариации амплитуды и частоты модулирующих сигналов. Для этого необходимо из папки Signals извлекать соответствующие файлы и находить их амплитудные спектры.

В) К каждой серии спектральных диаграмм написать вывод о влиянии изменяемого параметра сигнала (скважности импульсов, амплитуды и частоты модулирующего сигнала) на характер соответствующих спектров. Литература

1. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей.-Л.:Энергия, 1972.

2. Фельдбаум А.А. и др. Теоретические основы связи и управления. -М.:Ф.М., 1963.

3.Гоноровский Н.С. Радиотехнические цепи и сигналы.-М.: Сов. радио, 1971.

4.Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей.Л.:Энергия, 1972

⇐ Предыдущая 12