
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Владивосток. Составитель - А.С. Абрамов, доцент кафедры электроники
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ДАЛЬНЕВОСТОЧНЫЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СПЕКТРЫ
ПРОСТЫХ СИГНАЛОВ
Методические указания к лабораторной работе
Владивосток
Издательство Дальневосточного университета 2006
УДК 621.369
Настоящая работа содержит методические указания к выполнению лабораторной работы “Спектры простых сигналов”.
Пособие предназначено для студентов физического и геофизического факультетов, изучающих курс “Общая радиоэлектроника и электротехника”.
Составитель - А.С. Абрамов, доцент кафедры электроники
Печатается по решению кафедры электроники
ИФИТ ДВГУ
ã Издательство
Дальневосточного
Университета 2006.
1. Периодические сигналы ( краткие теоретические сведения )
Представление периодического сигнала в виде совокупности синусоидальных составляющих осуществляется с помощью рядов Фурье. Согласно теории Фурье сигнал 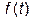 с периодом
с периодом 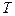 может быть представлен тригонометрическим рядом:
может быть представлен тригонометрическим рядом:
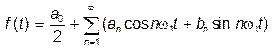 , (1)
, (1)
причем 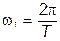 , а постоянные
, а постоянные 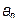 ,
, 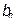 , называемые коэффициентами Фурье, определяются выражениями:
, называемые коэффициентами Фурье, определяются выражениями:
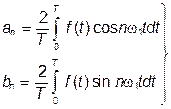 , где
, где 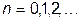 (2)
(2)
Этот ряд сходится, если исходная функция 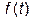 удовлетворяет условиям Дирихле:
удовлетворяет условиям Дирихле: 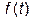 - ограничена и имеет на интервале
- ограничена и имеет на интервале 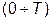 конечное число разрывов, а также максимумов и минимумов.
конечное число разрывов, а также максимумов и минимумов.
Ряд (1) можно записать в несколько иной форме:
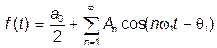 (3)
(3)
Совокупность гармонических составляющих, на которые разлагается функция 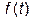 называется спектром, причем, как видно из (4), для полного задания спектра сигнала необходимо задать два подспектра - спектр амплитуд
называется спектром, причем, как видно из (4), для полного задания спектра сигнала необходимо задать два подспектра - спектр амплитуд 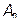 и спектр фаз
и спектр фаз 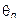 . Спектры принято изображать в виде линий, ортогональных к оси частот, длины которых пропорциональны
. Спектры принято изображать в виде линий, ортогональных к оси частот, длины которых пропорциональны 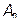 или
или 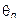 .
.
Составляющие спектра с 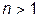 называются высшими гармониками. Их частоты кратны основной частоте сигнала
называются высшими гармониками. Их частоты кратны основной частоте сигнала
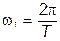 , (4)
, (4)
а интервал между любыми соседними гармониками постоянен (спектр эквидистантный) и численно равен 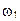 .
.
В зависимости от характера функции 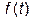 ряд (1) будет содержать только косинусоидальные, а для нечетной (
ряд (1) будет содержать только косинусоидальные, а для нечетной ( 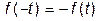 ) - синусоидальные члены. Для спектральных расчетов на практике чаще используют комплексную форму преобразований Фурье, которую легко получить из (1) и (2) представлением гармонических функций через показательные по известным формулам Эйлера
) - синусоидальные члены. Для спектральных расчетов на практике чаще используют комплексную форму преобразований Фурье, которую легко получить из (1) и (2) представлением гармонических функций через показательные по известным формулам Эйлера  , (5)
, (5)
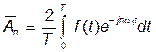 . (6)
. (6)
Здесь 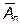 - комплексные амплитуды
- комплексные амплитуды 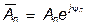 . (7)
. (7)
|
| |
| |
| |
| |
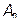 и
и 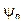 - соответственно, амплитуда и фаза
- соответственно, амплитуда и фаза 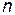 - ой гармоники.
- ой гармоники. 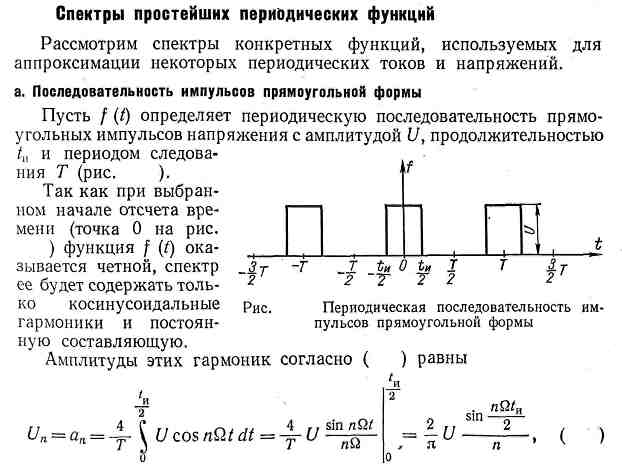
|
|
|
|
|
|

| |
|
|
|
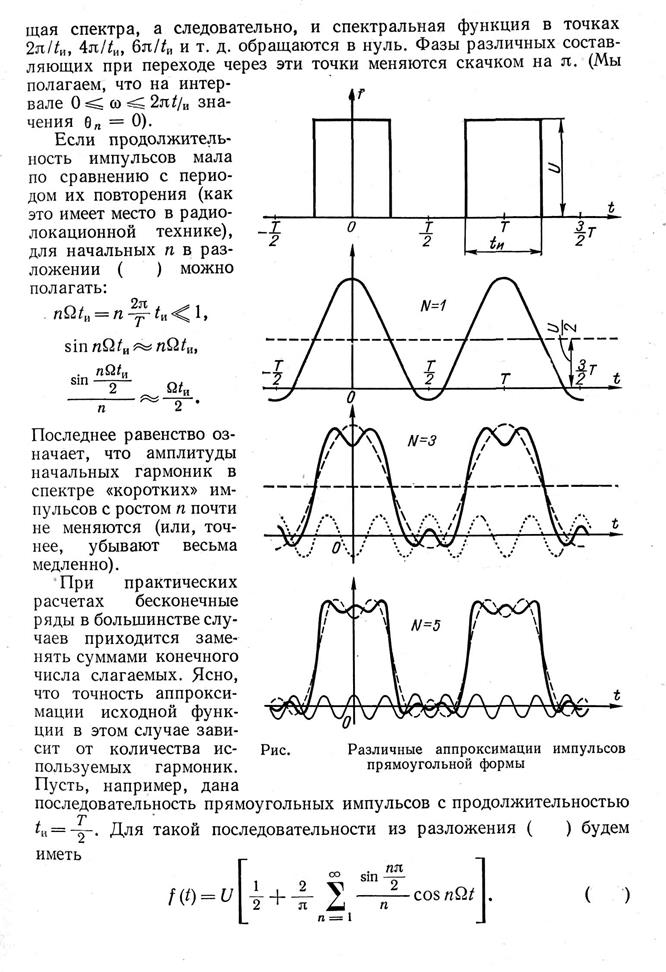
| |
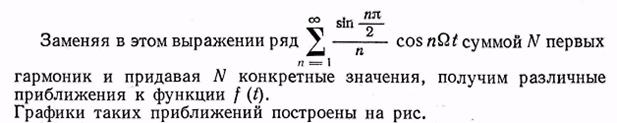
СПЕКТРЫ МОДУЛИРОВАННЫХ КОЛЕБАНИЙ
Для беспроводной передачи информации с помощью ВЧ–колебаний 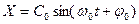 применяют модуляцию параметров этого колебания: амплитуды C0,частоты
применяют модуляцию параметров этого колебания: амплитуды C0,частоты 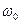 или фазы
или фазы 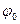 . Соответственно этому различают амплитудную(АМ), частотную(ЧМ) и фазовую(ФМ) модуляции.
. Соответственно этому различают амплитудную(АМ), частотную(ЧМ) и фазовую(ФМ) модуляции.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|