Fi⋅ δri + ΣRi⋅ δri + ΣΦi⋅ δri= 0

ΣFi⋅ δri + ΣRi⋅ δri + ΣΦi⋅ δri= 0

или

Σ(F_i + Φ_i)⋅ δr_i= 0,

которое и выражает общее уравнение динамики (принцип Даламбера-Лагранжа): при движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и сил инерции на любом возможном перемещении системы будет равна нулю.

Задача

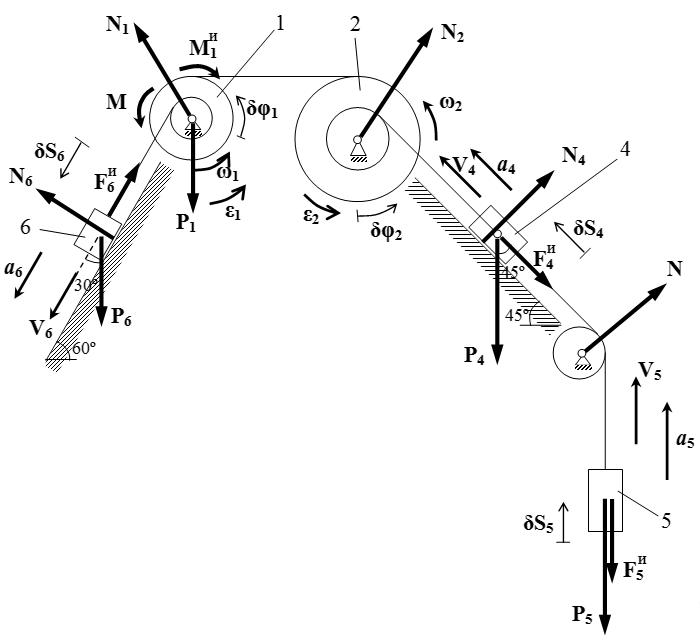
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м, приложенной к шкиву 1. Радиусы ступеней шкива 1 равны: R₁ = 0,2 м, r₁ = 0,1 м, а шкива 2 – R₂ = 0,3 м, r₂ = 0,15 м; их радиусы инерции относительно осей вращения равны соответственно ρ₁ = 0,1 м и ρ₂ = 0,2 м.

Пренебрегая трением, определить ускорение груза 5. Веса шкивов и грузов заданы: P₁ = 40 Н, P₂ = 0, P₃ = 0, P₄ = 20 Н, P₅ = 30 Н, P₆ = 10 Н. Грузы, веса которых равны нулю, на чертеже не изображать.

Указание. При решении задачи использовать общее уравнение динамики (принцип Даламбера – Лагранжа).

Дано: R1 = 0,2 м, r1 = 0,1 м, R2 = 0,3 м, r2 = 0,15 м, ρ1 = 0,1 м, ρ2 = 0,2 м. P1 = 40 Н, P2 = 0, P3 = 0, P4 = 20 Н, P5 = 30 Н, P6 = 10 Н, M = 10 Н·м.

Найти: a5.

Вопросы для самоконтроля представить вместе с развернутыми конспектами по данной теме с решением задач на эл почту bervengas@inbox.ru

Решение задачи выполнить в развернутом виде

⇐ Предыдущая 1 2 3 4 56