Вопросы для самоконтроля представить вместе с развернутыми конспектами по данной теме с решением задач на эл почту bervengas@inbox.ru

1. Что изучает динамика ? 2. В чем состоят первая и вторая задачи динамики ? 3. В чем смысл первой аксиомы динамики ? 4. Сформулируйте основной закон механики. 5. Запишите дифференциальное уравнение движения материальной точки. 6. Запишите дифференциальное уравнение движения материальной точки в естественных осях. 7. Что такое сила инерции и от чего зависит ее величина ? 8. Сформулируйте принцип Даламбера. В чем состоит его смысл ?

9.Что такое сила трения

Задача 1. Склон горы образует угол α с горизонтом. Под каким углом β к склону горы следует тянуть за веревку, чтобы равномерно тащить санки массой m в гору с наименьшим усилием? Какова должна быть эта сила? Коэффициент трения между санками и горой равен μ.

Задача 2. На наклонной плоскости, составляющей угол α с горизонтом, лежат одна на другой две доски. Возможны ли такие значения масс досок m₁ и m₂ и коэффициентов трения досок о плоскость μ₁ и друг о друга μ₂, при которых нижняя доска выскальзывала бы из-под верхней? В начальный момент доски покоятся.

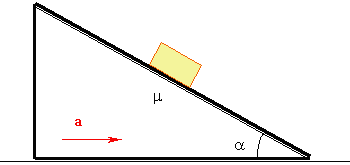
Задача 3. Клин, наклонная плоскость которого составляет угол α с горизонтом, движется с постоянным ускорением а вправо (рис. 5). Как будет двигаться лежащий на нем брусок, если коэффициент трения бруска о наклонную плоскость клина равен μ?

ПРИНЦИП ДАЛАМБЕРА-ЛАГРАНЖА

В принципе возможных перемещений говорится о необходимых и достаточных условиях равновесия системы с идеальными связями, то есть если система находится в равновесии, то сумма работ внешних сил, приложенных к точкам системы, на их возможном перемещении равна нулю:

ΣF_i⋅ δr_i=0 или

ΣF_i⋅ δS_i⋅ cosα_i=0.

Принцип Даламбера позволяет говорить о равновесии сил, действующих на точки системы (но не о равновесии системы). В эти силы входят: внешние силы, реакции связей, силы инерции, то есть

ΣF_i + ΣR_i + ΣΦ_i =0.

Объединяя эти два принципа (принцип Даламбера и принцип возможных перемещений), получаем для системы с идеальными связями уравнение

⇐ Предыдущая 1 2 3 456 Следующая ⇒