
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Напряженность магнитного поля. Магнитная индукция
Напряженность магнитного поля
Сила (H), с которой магнит действует на единицу магнитной массы, внесенную в его магнитное поле, называется напряженностью магнитного поля:
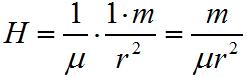 .
.
Где 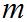 – магнитная масса данного магнита,
– магнитная масса данного магнита, 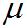 – коэффициент магнитной проницаемости среды. Так как для воздуха
– коэффициент магнитной проницаемости среды. Так как для воздуха 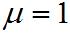 , то
, то
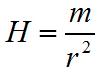 .
.
единица напряженности магнитного поля получается при 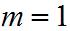 ,
, 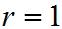 см и
см и 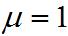 .
.
Направление напряженности магнитного поля совпадает с направлением силовых линий.
Магнитная индукция
Произведение 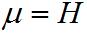 называют магнитной индукцией (направление индукции принимается совпадающим с направлением напряженности магнитного поля):
называют магнитной индукцией (направление индукции принимается совпадающим с направлением напряженности магнитного поля):
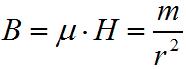
Единицей магнитной индукции служит «гаус» (индукция при µ=1 и H=1 или m=1 и r=1).
Магнитный поток (магнитный силовой поток)
Магнитным потоком Ф сквозь какую-либо замкнутую линию (контур), лежащую в плоскости перпендикулярной к направлению напряжения магнитного поля, называют произведение из индукции B на величину площади Q, ограничиваемой замкнутой линией
Ф =B • Q
Вместо того, чтобы говорить о магнитном потоке сквозь контур, можно говорить также о потоке сквозь поверхность, площадь, сечение, ограничиваемые этим контуром.
Понятие «магнитный поток» представляет аналогию с «расходом жидкости», текущей сквозь какое-либо сечение; расход жидкости измеряется произведением скорости жидкости на площадь сечения. Указанная аналогия облегчает понимание определения магнитного потока в более сложных случаях, соответствующих движению жидкости с неодинаковой скоростью и с неодинаковым направлением скорости в разных точках сечения (например, течение воды в расширяющемся русле реки).
Если плоскость замкнутой линии не перпендикулярна к направлению напряженности магнитного поля, а наклонна к нему, то выражение B• Q нужно помножить ещё на синус угла между плоскостью замкнутой линии и направлением напряженности магнитного поля.
Наконец, если контур не плоский и направление напряженности магнитного поля в разных местах контура (и внутри его) сильно изменяется (по направлению, по величине или по знаку), нужно заменить контур большим числом смежных небольших контуров, проведенных внутри рассматриваемого, каждый из которых можно принять за плоский. Тогда магнитным потоком сквозь рассматриваемый контур считается сумма магнитных потоков сквозь все такие «элементарные» контуры.
Пусть имеем магнитный полюс с массой 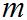 . Описав около него сферу радиуса
. Описав около него сферу радиуса 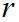 , получим, что полный поток, то есть магнитный поток сквозь эту замкнутую поверхность (сферу), будет равен произведению индукции
, получим, что полный поток, то есть магнитный поток сквозь эту замкнутую поверхность (сферу), будет равен произведению индукции 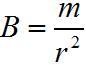 на площадь поверхности, то есть
на площадь поверхности, то есть 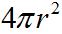 ; таким образом, полный поток в данном случае равен:
; таким образом, полный поток в данном случае равен:
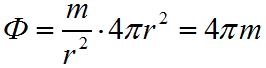 .
.
Можно доказать, что такую же величину мы получим для любой замкнутой поверхности, окружающей магнитный полюс, а не только для сферы, так что полный магнитный поток характеризует, так сказать, силу в данном случае магнитного полюса, и вообще – магнита, электромагнита и т.д.
Единицей магнитного потока служит «максвелл» – величина магнитного потока при 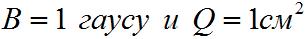 .
.
Выражение «магнитный поток» обычно ведёт к заблуждениям: в данном случае мы имеем дело лишь с особым состоянием среды, причем железные опилки только выявляют это состояние.
Определить магнитную массу одного из полюсов магнита, если общий поток равен 40000 единиц.
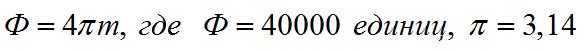 .
.
Следовательно
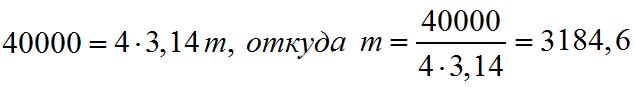 .
.
Чему равна магнитная индукция в вопросе предыдущего примера в расстоянии 5 см от полюса магнита?
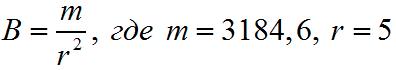
Следовательно
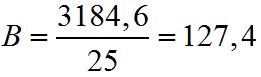 .
.
Магнитная масса северного полюса считается (условно) положительной и измеряется в положительных единицах, а южного – отрицательной с измерением в отрицательных единицах. Таким образом, в силу совместного существования полюсов всегда имеем
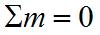
(то есть сумма всех магнитных масс = 0).
Определить магнитную индукцию у конца магнита, силовой поток которого через площадь концов его (4 X 5 см) равен 100000.
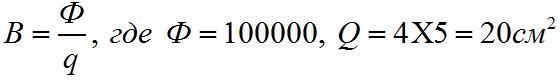
Следовательно
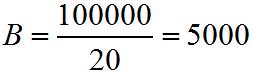 .
.
Определить величину полного магнитного потока сквозь площадь концов магнита, если магнитная индукция В равна 16000 единицам и размеры конца магнита 2 X 2,5 см
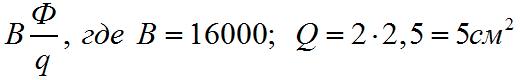
Следовательно
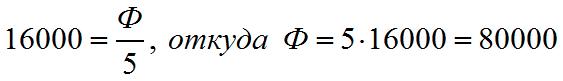 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|