
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО РАЗДЕЛУ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ» КУРСА ВЫСШЕЙ МАТЕМАТИКИ ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ФАКУЛЬТЕТА
Рекомендуемая литература
1. Венцель Е.С. Теория вероятностей. – М.: Наука, 1969-576с.
2. Виленкин Н.Я. Индукция. Комбинаторика. – М.: Просвещение, 1976-328с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1977-479с.
4. Румшиский Л.З. Элементы теории вероятностей. – М.: Наука, 1976-240с.
5. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и математической статистики. – М.: Наука, 1965-512с.
6. Феллер В. Введение в теорию вероятностей и ее приложения. М.: Мир, - т.1, 1984-258с.
КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО РАЗДЕЛУ «ТЕОРИЯ ВЕРОЯТНОСТЕЙ» КУРСА ВЫСШЕЙ МАТЕМАТИКИ ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ФАКУЛЬТЕТА
ВАРИАНТ 0
1.В лифт семиэтажного дома на первом этаже вошли три человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Найти вероятности следующих событий:
А = {все пассажиры выйдут на четвертом этаже},
В = {все пассажиры выйдут на одном и том же этаже},
С = {все пассажиры выйдут на разных этажах},
D = {хотя бы один из пассажиров выйдет на втором этаже},
Е = {два пассажира выйдут выше пятого этажа}.
2.В цехе работают 20 станков. Из них 10 станков марки А, 6 – марки В и 4 – марки С. Вероятность того, что качество детали окажется отличным, для станка марки А равна 0.9; для станка марки В – 0.8; марки С – 0.7. Каково процентное содержание числа деталей отличного качества во всей продукции цеха?
3.Монета бросается 80 раз. Какова вероятность того, что герб выпадет не менее 35 раз?
4.Из ящика, в котором 4 белых и 6 черных шаров, вынимают шары по одному без возврата до появления черного шара. Составить закон распределения случайной величины Х – числа появившихся белых шаров. Найти М(Х) и D(X).
5.Вес мотка пряжи – случайная величина, подчиненная нормальному закону с математическим ожиданием 100 г. Найти ее дисперсию, если отклонение веса мотка от среднего, превышающее 10 г, происходит с вероятностью 0.05.
6.Плотность распределения вероятностей непрерывной случайной величины Х имеет вид:
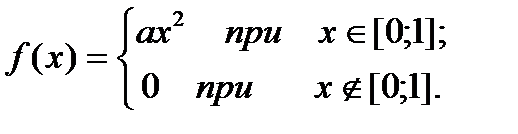
Найти а, М(Х), D(X), P (-1/2 < X < 1/2).
7.Найти коэффициент корреляции между величинами Х (вес алмазов в каратах) и Y (оптовая цена плоских шлифовальных алмазных кругов в тысячах рублей) на основании следующих данных:
| Х | 1.55 | 2.49 | 4.6 | 6.0 | 7.7 |
| Y |
Найти уравнения линейной регрессии Y на Х и X на Y. Начертить графики этих уравнений в одной системе координат. Сделать вывод о силе линейной зависимости между Х и Y .
ВАРИАНТ 1
1.Из партии, содержащей 10 деталей, среди которых 4 бракованные, наудачу извлекаются последовательно без возврата 3 детали. Найти вероятности следующих событий:
А = {все выбранные детали бракованные},
В = {среди выбранных деталей хотя бы одна бракованная},
С = {среди выбранных деталей ровно две бракованные},
D = {среди оставшихся деталей большинство бракованных},
Е = {две последние извлеченные детали бракованные}.
2.На фабрике, изготовляющей болты, первая машина производит 25%, вторая – 35%, третья – 40% всех изделий. В их продукции брак составляет соответственно 5, 4 и 2%. Какова вероятность того, что случайно выбранный болт является дефектным?
3.Игральная кость бросается 120 раз. Какова вероятность того, что 6 очков выпадут от 18 до 24 раз?
4.В ящике находятся 3 белых и 2 черных шара. Шары извлекаются по одному без возврата до появления черного шара. Составить закон распределения случайной величины Х – числа извлеченных шаров. Найти М(Х) и D(X).
5.Процент содержания крахмала в картофеле является нормально распределенной случайной величиной с математическим ожиданием 18% и средним квадратическим отклонением 3%. Найти вероятность того, что обе наудачу взятые картофелины содержат от 16% до 22% крахмала.
6.Дана функция распределения непрерывной случайной величины Х:
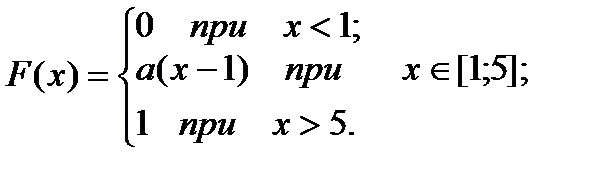
Найти а, М(Х), D(X), P (3 ≤ X < 6).
7.Найти коэффициент корреляции между величинами Х (рост производительности труда в промышленности СССР в процентах за пять лет с 1950 года) и Y (рост национального дохода в СССР в процентах за пять лет с 1950 года) на основании следующих данных:
| годы | ||||||
| Х | ||||||
| Y |
Найти уравнения линейной регрессии Y на Х и X на Y. Начертить графики этих уравнений в одной системе координат. Сделать вывод о силе линейной зависимости между Х и Y.
ВАРИАНТ 2
1. Из ящика, содержащего 5 деталей, среди которых 2 бракованные, наудачу последовательно и без возврата извлекаются детали до появления бракованной. Найти вероятности следующих событий:
А = {извлечено ровно две детали},
В = {извлечено не более трех деталей},
С = {извлечено более двух деталей},
D = {среди извлеченных деталей нет стандартной},
Е = {бракованных и стандартных деталей извлечено поровну}.
2. Два стрелка независимо друг от друга стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка равна 0.8, для второго – 0.4. После стрельбы в мишени обнаружена одна пробоина. Найти вероятность того, что в мишень попал первый стрелок.
3. Вероятность рождения мальчика равна 0.5. В семье 5 детей. Найти вероятность того, что в рассматриваемой семье мальчиков больше, чем девочек.
4. Буквы слова «ОГОРОД» рассыпаны в беспорядке. Из них выбирают 4 буквы. Найти математическое ожидание и дисперсию случайной величины Х – числа букв «О» среди выбранных. Найти М(Х) и D(X).
5. Размер детали подчинен нормальному закону с параметрами а = 30 микрон и σ = 5 микрон. Детали считаются годными, если размер детали находится в пределах от 20 до 40 микрон. Если размер детали больше 40 микрон, она подлежит переделке. Найти среднее число деталей, подлежащих переделке, из произведенных 1000 деталей.
6. Плотность распределения вероятностей непрерывной случайной величины Х имеет вид:
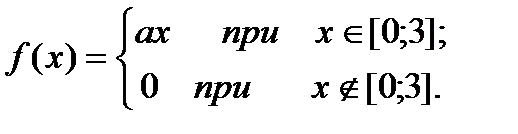
Найти а, М(Х), D(X), P (-1 < X < 1).
7. Найти коэффициент корреляции между величинами Х (вес изделий в килограммах) и Y (оптовая цена изделия из прозрачного кварцевого стекла в тысячах рублей) на основании следующих данных:
| Х | 1.5 | 1.8 | 2.1 | 2.4 | 2.9 |
| Y |
Найти уравнения линейной регрессии Y на Х и X на Y. Начертить графики этих уравнений в одной системе координат. Сделать вывод о силе линейной зависимости между Х и Y.
ВАРИАНТ 3
1. Вы останавливаете на улице наудачу трех человек и выясняете, в какой день недели они родились. Найти вероятности следующих событий:
А = {все родились в четверг},
В = {ни один не родился в воскресенье},
С = {все родились в различные дни недели},
D = {хотя бы один из опрошенных родился в понедельник},
Е = {все родились в один и тот же день недели}.
2.Вероятность того, что студент А решит задачу, равна 1/2; для студента В эта вероятность равна 1/3. Вызванный наудачу студент решил задачу. Какова вероятность того, что это был А?
3.Вероятность того, что саженец клена приживется, равна 0.6. Найти вероятность того, что из 600 саженцев число прижившихся окажется в пределах от 340 до 365.
4.Стрелок имеет 4 патрона и стреляет в цель до первого попадания. Вероятность попадания при каждом выстреле равна 0.8. Составить закон распределения случайной величины Х – числа использованных патронов. Найти М(Х) и D(X).
5.Заряд охотничьего пороха отвешивают на весах. Вес заряда - нормально распределенная случайная величина с параметрами а = 2.3 г и σ = 150 мг. Найти вероятность повреждения ружья при выстреле, если максимально допустимый вес заряда пороха равен 2.5 г.
6.Дана функция распределения непрерывной случайной величины Х:
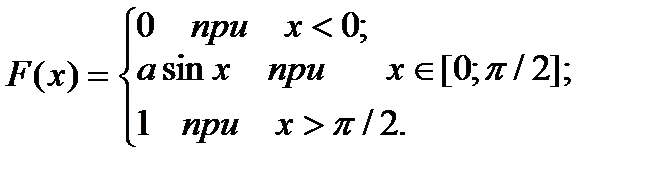
Найти а, М(Х), P (π/4 ≤ X < π).
7.Найти коэффициент корреляции между величинами Х (основные фонды пяти заводов СССР в 1950 г. в млн.рублей) и Y (выпуск продукции этих заводов в млн.рублей) на основании следующих данных:
| Х | |||||
| Y |
Найти уравнения линейной регрессии Y на Х и X на Y. Начертить графики этих уравнений в одной системе координат. Сделать вывод о силе линейной зависимости между Х иY.
ВАРИАНТ 4
1.С площади уезжают четыре автомобиля. Каждый автомобиль может с равной вероятностью поехать по любой из четырех улиц, начинающихся от этой площади. Найти вероятности следующих событий:
А = {все автомобили поедут по одной и той же улице},
В = {по каждой из улиц поедет автомобиль},
С = {по одной из улиц не поедет ни один из автомобилей},
D = {хотя бы по одной из улиц поедут более одного автомобиля},
Е = {хотя бы по одной из улиц поедут два автомобиля}.
2.Первый стрелок попадает в цель с вероятностью 0.8; второй – с вероятностью 0.6; третий – с вероятностью 0.5. Кто-то из них выстрелил в цель, но не попал. Какова вероятность того, что это был третий стрелок?
3.На каждые 10 изделий приходится в среднем одно дефектное. Найти вероятность того, что среди 36 взятых наудачу изделий 30 будут без дефектов.
4.Из ящика, в котором 8 белых и 2 черных шара, извлекаются сразу 3 шара. Составить закон распределения случайной величины Х – числа извлеченных черных шаров. Найти М(Х) и D(X).
5.Размер детали подчинен нормальному закону с параметрами а = 33 микрона и σ = 4 микрона. Поле допуска – от 20 микронов до 40 микронов. Найти вероятность брака.
6.Плотность распределения вероятностей непрерывной случайной величины Х имеет вид:
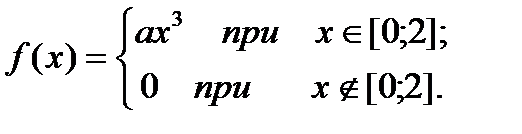
Найти а, М(Х), D(X), P (-1 < X < 1).
7.Найти коэффициент корреляции между величинами Х (глубина вспашки в см) и Y (величина урожая с 1 га) на основании следующих данных:
| Х | |||||
| Y | 9.0 | 8.5 | 9.2 | 9.6 | 9.4 |
Найти уравнения линейной регрессии Y на Х и X на Y. Начертить графики этих уравнений в одной системе координат. Сделать вывод о силе линейной зависимости между Х иY.
ВАРИАНТ 5
1.Наудачу набирается семизначный телефонный номер. Найти вероятности следующих событий:
А = {все цифры набранного номера различны},
В = {три последние цифры набранного номера совпадают},
С = {набранный номер начинается с цифры 5},
D = {хотя бы две цифры набранного номера совпадают},
Е = {все цифры набранного номера четные}.
2.Производственные мощности трех швейных фабрик относятся как 1:3:5. Процент брака изделий на фабриках равен соответственно 10%, 15%, 20%. Купленное изделие оказалось бракованным. Какова вероятность того, что это изделие изготовлено на второй фабрике?
3.Производится 240 выстрелов с вероятностью попадания при каждом выстреле, равной 0.7. Какова вероятность того, что произойдет не менее 160 попаданий?
4.Монета бросается до появления герба, но не более пяти раз. Составить закон распределения случайной величины Х – числа бросаний монеты. Найти М(Х) и D(X).
5.Автомат изготовляет шарики. Диаметр шарика – случайная величина, подчиненная нормальному закону. Известно, что в среднем у 92% шариков абсолютное отклонение диаметра от расчетного диаметра меньше 0.7 мм. Найти число шариков, у которых это отклонение будет меньше 1.08 мм, если изготовлено 1000 шариков.
6.Дана функция распределения непрерывной случайной величины Х:
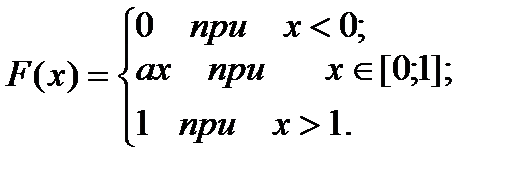
Найти а, М(Х), D(X), P (1/3 ≤ X < 4).
7.Найти коэффициент корреляции между величинами Х (энерговооруженность труда в квт/час на 1 человека) и Y (годовая выработка на одного работника в млн.рублей) на основании следующих данных:
| Х | |||||
| Y | 2.5 | 3.0 | 3.5 | 4.2 | 5.1 |
Найти уравнения линейной регрессии Y на Х и X на Y. Начертить графики этих уравнений в одной системе координат. Сделать вывод о силе линейной зависимости между Х и Y.
ВАРИАНТ 6
1.Вероятность попадания в цель при одном выстреле из орудия равна 0.9. Имея запас из пяти снарядов, ведут стрельбу по цели до первого попадания. Найти вероятности следующих событий:
А = {произведено четыре выстрела},
В = {число промахов и число попаданий совпадают},
С = {попадание произошло не позже, чем при третьем выстреле},
D = {весь запас снарядов израсходован},
Е = {стрельба произведена без промахов}.
2.Партия беретов уложена в 100 коробках, причем 10 коробок содержат по 60% белых беретов, 50 коробок содержат по 70% белых беретов, остальные – по 20% белых беретов. Из наудачу взятой коробки наудачу вынули берет. Он оказался белым. Найти вероятность того, что он вынут из коробки, содержащей 20% белых беретов.
3.Наблюдениями в некоторой местности установлена вероятность того, что день будет безоблачным. Она равна 0.25. Найти вероятность того, что в течение недели число безоблачных дней будет не больше трех.
4.В I ящике - 2 белых и 3 черных шара, во II ящике – 3 белых и 3 черных шара. Из каждого ящика вынимают по одному без возврата 2 шара. Случайная величина Х – число вынутых белых шаров. Найти М(Х) и D(X).
5.Рост человека из некоторой совокупности подчинен нормальному закону с параметрами а = 176 см и σ = 8 см. Какова вероятность того, что двое выбранных наудачу людей имеют рост выше 172 см?
6.Плотность распределения вероятностей непрерывной случайной величины Х имеет вид:
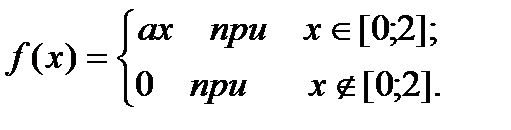
Найти а, М(Х), D(X), P (-2 < X < 1).
7.Найти коэффициент корреляции между величинами Х (основные фонды во всех отраслях народного хозяйства СССР в процентах к 1950 году) и Y (численность рабочих и служащих, занятых в народном хозяйстве СССР в процентах к 1950 году) на основании следующих данных:
| годы | ||||||
| Х | ||||||
| Y |
Найти уравнения линейной регрессии Y на Х и X на Y. Начертить графики этих уравнений в одной системе координат. Сделать вывод о силе линейной зависимости между Х и Y.
ВАРИАНТ 7
1.Два баскетболиста по очереди бросают мяч в корзину, при этом каждый может сделать не более трех бросков. Выигрывает тот, кто первым забросит мяч. Вероятности попадания при одном броске для первого и второго баскетболиста равны соответственно 0.8 и 0.6. Найти вероятности следующих событий:
А = {выиграл первый баскетболист},
В = {второй баскетболист сделал не менее одного броска},
С = {каждый из баскетболистов сделал ровно по одному промаху},
D = {баскетболисты сделали одинаковое число бросков},
Е = {при игре было произведено меньше пяти бросков}.
2.Имеются 2 ящика I типа, 3 ящика II типа и 4 ящика III типа. Ящик I типа содержит 5 шаров: 2 белых и 3 черных; ящик II типа – 4 шара: 3 белых и 1 черный; III типа – 6 шаров: 2 белых и 4 черных. Из наудачу взятого ящика наудачу вынули шар. Он оказался белым. Найти вероятность того, что он был вынут из ящика III типа.
3.В среднем в час происходит 120 обрывов на 1000 веретен. Найти вероятность того, что на 100 веретенах в час произойдет от 10 до 14 обрывов.
4.Игральная кость бросается 4 раза. Составить закон распределения случайной величины Х – числа появлений четного числа очков. Найти М(Х) и D(X).
5.Производится стрельба по полосе шириной 20 м с прицеливанием по ее средней линии. Отклонение от средней линии – нормально распределенная случайная величина со средним квадратическим отклонением 16 м. Найти вероятность попадания в полосу при одном выстреле.
6.Плотность распределения вероятностей непрерывной случайной величины Х имеет вид:
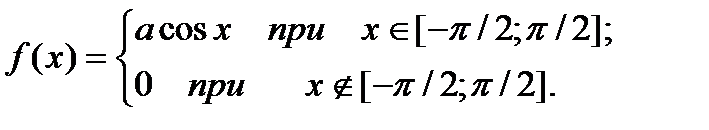
Найти а, М(Х), P (0 < X < π).
7.Найти коэффициент корреляции между величинами Х (основные фонды во всех отраслях народного хозяйства СССР в процентах к 1950 году) и Y (валовая продукция всей промышленности СССР в процентах к 1950 году) на основании следующих данных:
| годы | ||||||
| Х | ||||||
| Y |
Найти уравнения линейной регрессии Y на Х и X на Y. Начертить графики этих уравнений в одной системе координат. Сделать вывод о силе линейной зависимости между Х и Y.
ВАРИАНТ 8
1.Игральная кость бросается четыре раза. Найти вероятности следующих событий:
А = {ни разу не выпало 6 очков},
В = {каждый раз выпадало одно и то же число очков},
С = {хотя бы один раз выпало 2 очка},
D = {сумма выпавших очков равна пяти},
Е = {все числа выпавших очков оказались различными}.
2.В коробке 10 револьверов, среди которых 6 пристрелянных. Вероятность попасть в цель при одном выстреле из пристрелянного револьвера равна 0.9, из непристрелянного – 0.7. Найти вероятность того, что в результате выстрела из наудачу взятого револьвера произойдет попадание.
3.Семена данного сорта всходят с вероятностью 0.8. Какова вероятность того, что из 90 посеянных семян взойдут не менее 70?
4.В соревнованиях участвуют 3 спортсмена. Вероятности выигрыша для них равны соответственно 0.4; 0.7; 0.8. Найти математическое ожидание и дисперсию числа выигравших спортсменов.
5.Вес изделия распределен по нормальному закону. Известно, что абсолютные отклонения веса изделия от его расчетного веса, превосходящие 150 г, встречаются в среднем 31 раз на 1000 изделий. Найти параметр σ распределения веса изделия.
6.Плотность распределения вероятностей непрерывной случайной величины Х имеет вид:
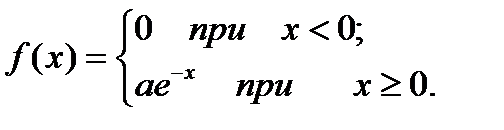
Найти а, М(Х), D(X), P (-1 < X < 1).
7.Найти коэффициент корреляции между величинами Х (валовый отечественный продукт в млрд. франков) и Y (импорт в млрд. франков) по данным периода 1949-1966 гг. во Франции, представленным в следующей таблице:
| Х | 149.3 | 161.2 | 171.5 | 175.5 | 180.8 | 190.7 |
| Y | 15.9 | 16.4 | 19.0 | 19.1 | 18.8 | 20.4 |
Найти уравнения линейной регрессии Y на Х и X на Y. Начертить графики этих уравнений в одной системе координат. Сделать вывод о силе линейной зависимости между Х и Y.
ВАРИАНТ 9
1.В лотерее из 10 билетов 4 выигрышных. Пять человек приобрели по одному билету. Найти вероятности следующих событий:
А = {никто из игравших не выиграл},
В = {хотя бы один из игравших выиграл},
С = {выиграли ровно двое из игравших},
D = {число проигравших меньше числа выигравших},
Е = {среди оставшихся билетов большинство выигрышных}.
2.В первой колоде 32 карты, во второй – 52 карты. Из первой колоды во вторую переложили две карты. После этого из второй колоды вынули 1 карту. Найти вероятность того, что вынут туз.
3.Вероятность попадания баскетболистом в корзину при одном броске равна 2/3. Произведено 4 броска по корзине. Найти вероятность того, что произошло не менее трех попаданий.
4.Вероятность попадания в цель при одном выстреле для стрелков А, В, С равны соответственно 0.9; 0.7; 0.6. Каждый стрелок произвел по одному выстрелу. Составить закон распределения случайной величины Х – числа происшедших при этом попаданий в цель. Вычислить М(Х) и D(X).
5.Вес рыб, вылавливаемых из пруда, подчинен нормальному закону с параметрами а = 375 г и σ = 25 г. Найти вероятность того, что вес выловленной рыбы не менее 300 г.
6.Плотность распределения вероятностей непрерывной случайной величины Х имеет вид:
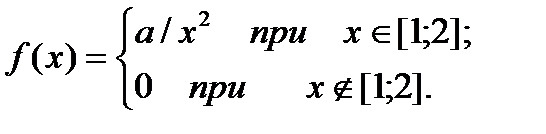
Найти а, М(Х), D(X), P (0 < X < 3/4).
7.Найти коэффициент корреляции между величинами Х (темпы прироста производительности труда) и Y (темпы прироста продукции по данным Госкомстата СССР за 1987 год) на основании данных, приведенных в следующей таблице:
| Х | 3.9 | 3.1 | 6.1 | 3.5 | 1.9 | 3.6 |
| Y | 3.3 | 2.6 | 6.4 | 3.7 | 2.5 | 4.4 |
Найти уравнения линейной регрессии Y на Х и X на Y. Начертить графики этих уравнений в одной системе координат. Сделать вывод о силе линейной зависимости между Х и Y.
ПРОГРАММА И КОНТРОЛЬНЫЕ ЗАДАНИЯ
ПО КУРСУ ВЫСШЕЙ МАТЕМАТИКИ
(ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА)
ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
Редактор Т.Ф. Морозова
Лицензия ЛР № 020412 от 12.02.92
Подписано в печать 04.09.95. Формат 60х84 1/16.
Бум.кн.-журн. Печ.л. 1.0. Бум.л. 0,5. РТП изд-ва СПбУЭФ
Тираж 1000. Зак. 502
Издательство Санкт-Петербургского университета экономики и финансов
191023, Санкт-Петербург, Садовая ул., д. 21
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|