
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания.
Дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат ее математического ожидания.
Вычислим значение дисперсии
для случайной величины Х, рассмотренной в примере 1.
По первой формуле:
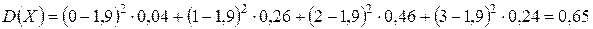 .
.
По второй формуле:
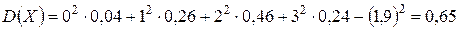 .
.
Следует помнить, что, по своему определению, дисперсия — величина неотрицательная, т. е. 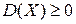 .
.
2) Среднеквадратическим отклонением 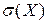 случайной величины Х называется корень квадратный из дисперсии:
случайной величины Х называется корень квадратный из дисперсии:
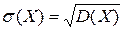 . (
. ( 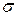 -«сигма», буква греч. алфавита )
-«сигма», буква греч. алфавита )
Характеристика вводится, чтобы иметь возможность указать разброс в той же размерности, что и сама случайная величина (т. к. дисперсия имеет размерность квадрата Х).
Для нашего примера 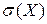 = 0,81.
= 0,81.
Среднеквадратическое отклонение имеет смысл абсолютной погрешности при замене Х ее математическим ожиданием.
3) Вариацией 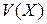 случайной величины Х называется отношение
случайной величины Х называется отношение 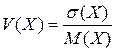 .
.
Вариация имеет смысл относительной погрешности.
7.4. Способы представления непрерывной случайной величины
Пусть НСВ (непрерывная случайная величина) Х принимает значения из некоторого промежутка 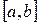 .
.
Значения 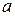 и
и 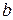 , в зависимости от конкретных условий, могут быть различными, а сам промежуток
, в зависимости от конкретных условий, могут быть различными, а сам промежуток 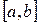 может быть конечным (например, [–1,2]), полубесконечным (например, (-
может быть конечным (например, [–1,2]), полубесконечным (например, (- 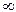 ,0] или [3,
,0] или [3, 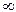 )) или бесконечным
)) или бесконечным 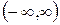 . Подразумевается, что
. Подразумевается, что 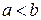 .
.
Все значения, попадающие на 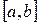 , невозможно перечислить,
, невозможно перечислить,
поэтому невозможно и указать, какие вероятности им соответствуют.
Чтобы охарактеризовать распределение вероятностей в этом случае, поступают так. На 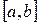 выделяют участок от
выделяют участок от 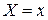 до
до 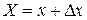 и находят отношение вероятности попадания на этот участок
и находят отношение вероятности попадания на этот участок 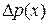 к длине участка:
к длине участка:
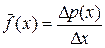 .
.
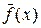 представляет собой среднюю вероятность, приходящуюся на единицу измерения Х, вычисленную на участке
представляет собой среднюю вероятность, приходящуюся на единицу измерения Х, вычисленную на участке 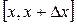 .
.
По аналогии с плотностью (массой, приходящейся на единицу объема) она может быть названа средней плотностью вероятности. Средняя плотность вероятности зависит и от положения точки 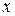 , и от длины участка
, и от длины участка 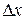 . Чтобы исключить влияние
. Чтобы исключить влияние 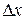 , его стараются взять как можно меньшим, т. е. находят предел:
, его стараются взять как можно меньшим, т. е. находят предел:
.
Функция 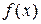 называется плотностью вероятности (или плотностью распределения вероятности).
называется плотностью вероятности (или плотностью распределения вероятности).
Она должна удовлетворять следующему требованию:
.
График функции плотности вероятности называется кривой распределения.
Как и для ДСВ, вводится понятие функции распределения: 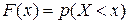 .
.
Между функциями 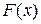 и
и 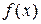 имеется тесная связь:
имеется тесная связь:
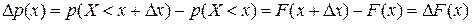 ;
;
.
ü Итак, плотность вероятности 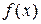 является производной от функции распределения
является производной от функции распределения 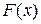 и, наоборот,
и, наоборот,
ü функция распределения 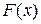 является первообразной для плотности вероятности, ее можно найти по формуле:
является первообразной для плотности вероятности, ее можно найти по формуле:
.
В связи с этим,
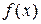 называют иногда дифференциальной функцией распределения,
называют иногда дифференциальной функцией распределения,
а 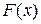 — интегральной.
— интегральной.
Свойства функции 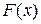 для НСВ аналогичны свойствам функции распределения для ДСВ.
для НСВ аналогичны свойствам функции распределения для ДСВ.
С помощью функции распределения можно найти вероятность попадания значений случайной величины 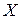 на промежуток
на промежуток 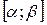 :
:
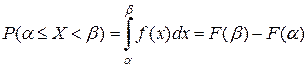 .
.
7.5. Числовые характеристики НСВ
Числовые характеристики для НСВ те же самые, что и для ДСВ, и аналогичны им по смыслу, однако вычисляются несколько иначе.
1) Математическим ожиданием 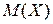 НСВ называется значение, определяемое следующей формулой:
НСВ называется значение, определяемое следующей формулой: 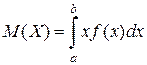 .
.
2) Модой 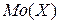 НСВ называется значение Х, соответствующее максимуму функции
НСВ называется значение Х, соответствующее максимуму функции 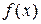 . Если максимум один, то распределение называется унимодальным, если максимумов несколько, то полимодальным. Например, при двух максимумах распределение называется бимодальным.
. Если максимум один, то распределение называется унимодальным, если максимумов несколько, то полимодальным. Например, при двух максимумах распределение называется бимодальным.
3) Медианой 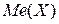 НСВ называется ее значение, для которого выполняется условие:
НСВ называется ее значение, для которого выполняется условие: 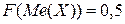 .
.
4) Дисперсией 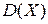 непрерывной случайной величины Х называется математическое ожидание квадрата отклонения Х от М(Х), вычисляемое по формуле
непрерывной случайной величины Х называется математическое ожидание квадрата отклонения Х от М(Х), вычисляемое по формуле
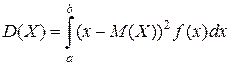 .
.
Как и в случае с ДСВ, дисперсия может быть вычислена по более простой формуле:
.
5) Среднеквадратическое отклонение 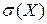 НСВ равно корню квадратному из дисперсии:
НСВ равно корню квадратному из дисперсии: 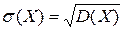 .
.
6) Вариацией или коэффициентом вариации 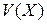 НСВ называется
НСВ называется
отношение: 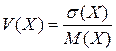 .
.
Пример 2. Точку бросают наугад внутрь круга радиуса  . Охарактеризовать случайную величину
. Охарактеризовать случайную величину  – расстояние от точки до центра круга.
– расстояние от точки до центра круга.
Решение. Очевидно, что 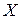 может принимать любые значения в промежутке
может принимать любые значения в промежутке 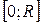 . Чтобы найти вид функции
. Чтобы найти вид функции 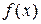 , составим соответствующий предел.
, составим соответствующий предел.
Изменению значений 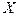 от
от 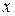 до
до 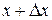 соответствует попадание точки внутрь кольца, ограниченного окружностями с радиусами
соответствует попадание точки внутрь кольца, ограниченного окружностями с радиусами 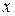 и
и 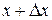 . Вероятность попадания на этот участок
. Вероятность попадания на этот участок 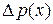 согласно геометрическому определению вероятности равна отношению площади этого участка к площади всего круга:
согласно геометрическому определению вероятности равна отношению площади этого участка к площади всего круга:
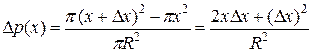 .
.
Тогда 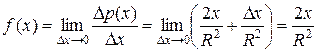 .
.
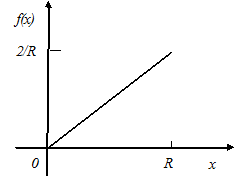
Полученной формулой для плотности вероятности можно пользоваться, если 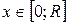 . Для остальных значений аргумента она равна 0. Окончательно:
. Для остальных значений аргумента она равна 0. Окончательно:
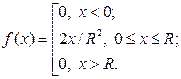 или
или 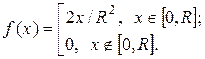
Найдём вид функции распределения, пользуясь формулой 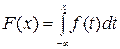 и учитывая, что функция плотности вероятности имеет различный вид на разных промежутках: а)
и учитывая, что функция плотности вероятности имеет различный вид на разных промежутках: а)  ,
, 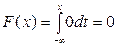 .
.
б) 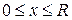 ,
, 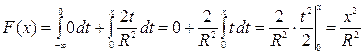 .
.
в) 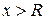 ,
, 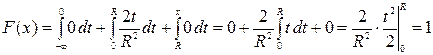 .
.
Окончательно: 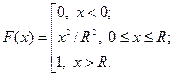
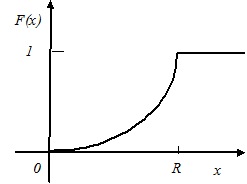
Графики обеих функций представлены на рисунке 2.
.
.
Рис.2
Математическое ожидание 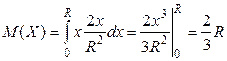
Моды у данной случайной величины нет, т.к. у функции 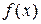 нет максимума.
нет максимума.
Из условия 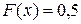 находим медиану
находим медиану 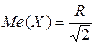 .
.
Вычислим дисперсию: 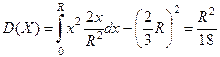 .
.
Среднеквадратическое отклонение 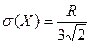 , вариация
, вариация 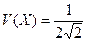 .
.
Пример 3. Дана функция распределения НСВ Х:

Решение. Используем связь функции плотности вероятности с функцией распределения вероятностей: 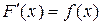 .
.
На рисунках представлены графики:
функции распределения вероятностей 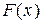 и плотности вероятностей
и плотности вероятностей 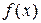 .
.
 ********************************************************************************
********************************************************************************
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|