
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция 7.Случайные величины. Числовые характеристики
Лекция 7.Случайные величины. Числовые характеристики
7.1. Определение и виды случайных величин
Очень часто на практике приходится иметь дело с величинами, значения которых нельзя предсказать заранее.
Такими величинами являются, например,
 число клиентов, обратившихся в банк в течение дня,
число клиентов, обратившихся в банк в течение дня,
 количество попаданий в мишень при нескольких выстрелах,
количество попаданий в мишень при нескольких выстрелах,
 расстояние от точки попадания до центра мишени,
расстояние от точки попадания до центра мишени,
 количество осадков за определенный промежуток времени и т. д.
количество осадков за определенный промежуток времени и т. д.
На каждую из этих величин действует большое количество мелких факторов, которые трудно, иногда и невозможно, а иногда и не нужно учитывать по отдельности. Например, на полет снаряда, кроме основных — калибра орудия, величины заряда и наводки — влияют скорость и направление ветра, плотность воздуха, зависящая от температуры, осадки и т. п. Поскольку сами эти факторы не остаются неизменными, то и их влияние на определяемую в опыте величину будет также меняться. В результате от опыта к опыту будет получаться несколько иное значение измеряемой величины.
Случайной называется переменная величина, значения которой зависят от случайного исхода опыта.
Некоторые из случайных величин, например, число клиентов в банке, количество попаданий в мишень, могут принимать отдельные, изолированные значения, которые можно перечислить.
Случайная величина, которая может принимать значения некоторой конечной или бесконечной числовой последовательности, называется дискретной(краткое обозначение ДСВ).
Случайная величина, которая может принимать любые значения из некоторого промежутка или промежутков, называется непрерывной (краткое обозначение НСВ).
Непрерывной случайной величиной является, например, количество осадков или расстояние от точки попадания до центра мишени.
Случайные величины принято обозначать большими латинскими буквами 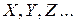 ...
...
Чтобы описать случайную величину, нужно не только знать, какие значения она принимает, но и как часто, т. е. с какой вероятностью встречаются те или иные значения.
В опыте случайная величина обязательно примет одно из своих значений, поэтому полная (суммарная) вероятность равна 1.
То, как эта полная вероятность поделена между различными значениями случайной величины, называется распределением случайной величины.
Способы описания распределения для ДСВ и НСВ несколько различны, поэтому рассмотрим их отдельно.
7.2. Способы представления дискретной случайной величины
Законом распределения ДСВ называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Таблица, в которой представлены значения 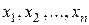 случайной величины
случайной величины 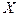 и соответствующие им вероятности
и соответствующие им вероятности 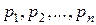 (т. е. вероятности того, что
(т. е. вероятности того, что 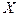 примет значение, равное
примет значение, равное 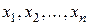 ), называется рядом распределения. Если в таблице учтены все возможные значения
), называется рядом распределения. Если в таблице учтены все возможные значения 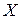 , то должно выполняться условие
, то должно выполняться условие
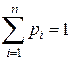 .
.
Информация о распределении, представленная на графике точками с координатами ( 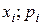 ) и соединяющей их ломаной, называется многоугольником (полигоном) распределения.
) и соединяющей их ломаной, называется многоугольником (полигоном) распределения.
Вероятность того, что случайная величина 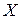 примет значение, меньшее
примет значение, меньшее 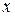 , называется функцией распределения
, называется функцией распределения 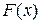 , т. е.
, т. е. 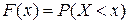 .
.
Для ДСВ 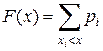 .
.
Пример 1. Батарея состоит из 3 орудий. Вероятность попадания в цель при одном выстреле для первого орудия 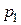 = 0,5; для второго
= 0,5; для второго 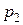 = 0,6; для третьего —
= 0,6; для третьего — 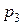 = 0,8. Все орудия делают по одному выстрелу.
= 0,8. Все орудия делают по одному выстрелу.
Охарактеризовать случайную величину Х — число попаданий в цель.
(Примечание. Характеристика дискретной случайной величины Х изпримера 1 будет проводиться в п.п. 7.2 и 7.3, поэтому целесообразно для этой задачи отвести полный разворот тетради и заполнять его по мере описания всех характеристик.)
Решение.
Очевидно, что величина Х может принять одно из четырех значений: 0, 1, 2, 3.
Рассмотрим 4 случая:
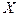 = 0, если ни одно орудие не попадет;
= 0, если ни одно орудие не попадет;
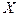 = 1, если попадет одно орудие (либо первое, либо второе, либо третье);
= 1, если попадет одно орудие (либо первое, либо второе, либо третье);
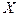 = 2, если попадут два орудия: либо первое и второе, либо первое и третье, либо второе и третье;
= 2, если попадут два орудия: либо первое и второе, либо первое и третье, либо второе и третье;
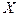 = 3, если попадут все три орудия.
= 3, если попадут все три орудия.
Найдём вероятности событий в каждом случае:
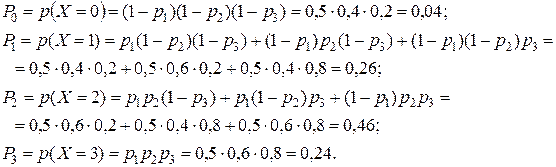
Сделаем проверку: 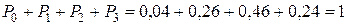 .
.
Выпишем ряд распределения в виде таблицы:
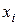
| ||||
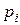
| 0,04 | 0,26 | 0,46 | 0,24 |
Полигон (многоугольник) распределения представлен на рисунке 1, где на координатной плоскости нанесены точки с координатами 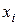 по оси Х и
по оси Х и 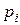 по оси У. Для наглядности эти точки соединены отрезками прямых.
по оси У. Для наглядности эти точки соединены отрезками прямых.
Функция распределения представлена таблицей и графиком, рис.1.
Мы знаем, что функцией распределения 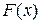 называется
называется 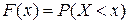 , т. е. вероятность того, что случайная величина
, т. е. вероятность того, что случайная величина 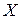 примет значение, меньшее
примет значение, меньшее 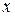 .
.
Для того, чтобы составить функцию распределения, всю числовую ось разбивают на промежутки значениями случайной величины. Из каждого промежутка берут произвольное значение аргумента и находят значение функции распределения, пользуясь её определением.
Для х ≤0 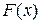 =0, т.к. значений х<0 эта величина не имеет;
=0, т.к. значений х<0 эта величина не имеет;
если 0<х ≤1, 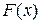 =0,04, т.к. для таких х меньшим является одно значение х=0, вероятность которого 0,04;
=0,04, т.к. для таких х меньшим является одно значение х=0, вероятность которого 0,04;
если 1<х ≤2, 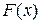 =0,04+0,26=0,3, это вероятность, с которой ДСВ Х принимает значения, меньшие 2, т.е. 0 или 1;
=0,04+0,26=0,3, это вероятность, с которой ДСВ Х принимает значения, меньшие 2, т.е. 0 или 1;
если 2 <х ≤3, 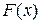 =0,3+0,46=0,76, это вероятность всех значений, меньших 3, т.е. 0, 1 или 2;
=0,3+0,46=0,76, это вероятность всех значений, меньших 3, т.е. 0, 1 или 2;
если х>3, 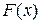 = 0,76+ 0,24=1, т.к. все возможные значения Х не больше 3-х.
= 0,76+ 0,24=1, т.к. все возможные значения Х не больше 3-х.
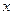
| 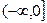
| 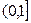
| 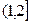
| 
| 
|
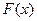
| 0,04 | 0,3 | 0,76 |
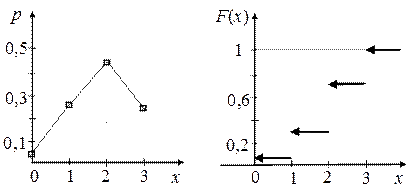 Рис.1.
Рис.1.
Обратите внимание: т.к. при х ≤0 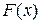 =0, то график при этих х совпадает с отрицательной полупрямой оси Х; график при х, больших 3, представляет собой луч, параллельный оси Х с выколотым началом в точке (3,1);участки графика на полуинтервалах
=0, то график при этих х совпадает с отрицательной полупрямой оси Х; график при х, больших 3, представляет собой луч, параллельный оси Х с выколотым началом в точке (3,1);участки графика на полуинтервалах 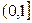 ,
, 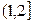 ,
, 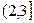 - горизонтальные отрезки с выколотыми левыми концами и включёнными правыми.
- горизонтальные отрезки с выколотыми левыми концами и включёнными правыми.
Данный пример иллюстрирует следующие
свойства функции распределения ДСВ (которые можно легко доказать, учитывая, что вероятность любого события заключена в пределах от 0 до 1).
1) 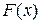 – ступенчатая разрывная функция;
– ступенчатая разрывная функция;
2) 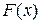 – неубывающая функция (т. е. либо возрастает, либо постоянна);
– неубывающая функция (т. е. либо возрастает, либо постоянна);
3) 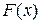 = 0, для всех
= 0, для всех 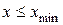 , где
, где 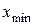 – наименьшее из всех значений
– наименьшее из всех значений 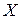 ;
;
4) 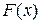 = 1, для всех
= 1, для всех 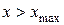 , где
, где 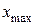 – наибольшее из всех значений
– наибольшее из всех значений 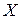 .
.
Приведенные характеристики дают полное и ясное представление о случайной величине. Однако, в случае, когда ДСВ имеет много значений (десятки, сотни и т. д.) они будут очень громоздкими и требуют много места.
Кроме того, во многих практических задачах вовсе нет необходимости так подробно описывать случайную величину.
7.3. Числовые характеристики ДСВ
Числовые характеристики служат для краткого описания ДСВ
и делятся на две группы:
характеристики положения и характеристики разброса.
К характеристикам положения относятся математическое ожидание, мода и медиана случайной величины.
Дадим их определения:
1) Математическим ожиданием 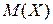 дискретной случайной величины
дискретной случайной величины 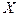 называется значение, определяемое следующей формулой:
называется значение, определяемое следующей формулой:
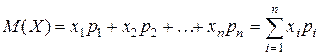 .
.
Математическое ожидание представляет собой средневзвешенное всех значений Х (“весами” служат вероятности отдельных значений) и характеризует порядок величины (десятые, сотые, целые числа, десятки, сотни и т. д.).
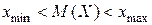 .
.
Найдём математическое ожидание 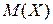 случайной величины Х из разобранного в данном разделе примера 1.
случайной величины Х из разобранного в данном разделе примера 1.
Используем ряд распределения в виде таблицы:
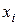
| ||||
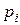
| 0,04 | 0,26 | 0,46 | 0,24 |
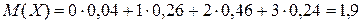 .
.
2) Модой 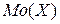 случайной величины называется ее значение, имеющее наибольшую вероятность. В нашем примере
случайной величины называется ее значение, имеющее наибольшую вероятность. В нашем примере 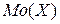 = 2.
= 2.
3) Медианой 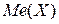 случайной величины называется такое ее значение, для которого выполняется следующее условие:
случайной величины называется такое ее значение, для которого выполняется следующее условие:
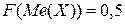
Т.е., медиана — такое значение случайной величины, для которого функция распределения равна 0.5. (В нашем примере медианы нет.)
Рассмотрим теперь характеристики разброса.
К характеристикам разброса относятся дисперсия,среднеквадратическое отклонение и вариация.
Необходимость их введения можно пояснить на примере.
Пусть заданы две случайные величины 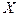 и
и 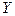 .
.
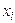
| |||||
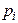
| 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
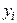
| – 10 | ||||
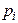
| 0,2 | 0,2 | 0,2 | 0,2 | 0,2 |
По данным из таблицы найдем математическое ожидание
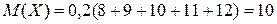 ,
,
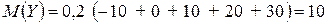 .
.
Видно, что при одной и той же величине математического ожидания, отдельные значения 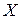 отличаются от
отличаются от 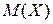 гораздо меньше, чем отдельные значения
гораздо меньше, чем отдельные значения 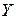 от
от 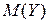 . Числовые характеристики, определения которых сейчас будут даны, учитывают эту разницу в поведении случайных величин.
. Числовые характеристики, определения которых сейчас будут даны, учитывают эту разницу в поведении случайных величин.
1) Дисперсией 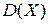 случайной величины Х называется математическое ожидание квадрата отклонения Х от своего математического ожидания.
случайной величины Х называется математическое ожидание квадрата отклонения Х от своего математического ожидания.
(Термин «дисперсия» означает рассеяние.)
Для ДСВ дисперсия вычисляется по формуле:
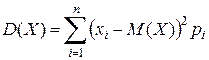 .
.
Преобразование этой формулы позволяет привести ее к более удобному виду:
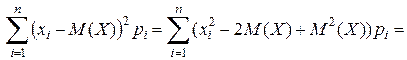
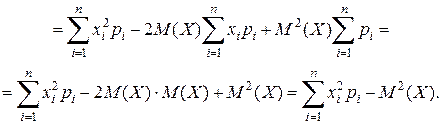
Используя аналогию с 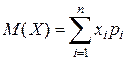 можно обозначить
можно обозначить 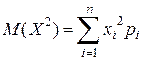 .
.
Тогда 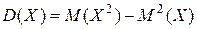 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|