Контакты

Случайная статья

X^4 + x^3( α ^8+ α ^4+ α ^2+ α) + x^2 (α ^12+ α ^10+ α ^9+ α ^6+ α ^5+ α ^3) + x*( α ^14+ α ^12+ α ^11+ α ^7) + α ^15 = x^4 + x + 1. с = (сn-1, cn-2,…, c1,c0). с’ = (сn-2, cn-3,

⇐ ПредыдущаяСтр 2 из 2

x^(q^m – 1) - 1 = 0

(q^m – 1)

X^2 +1 = 0 = (x-i)(x+i)

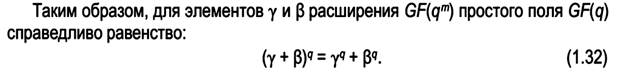
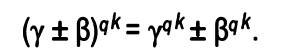
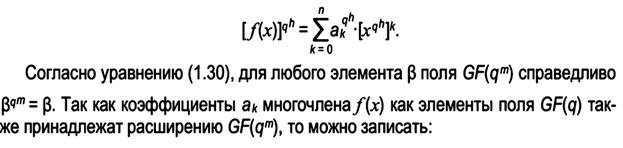
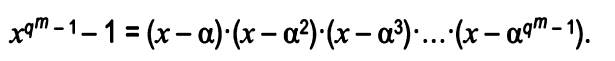
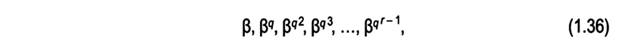
P(x) = x^3 + x + 1

q=2

α α^2 α^4

GF(2^4) p(x) = x^4 + x+ 1

x^15 + 1 = (x-1)(x-α)( x-α^2)…. = f1(x)*f2(x)*…*f(k)

α α^2 α^4 α^8

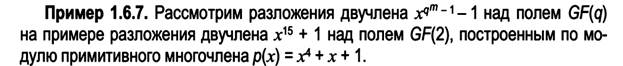
https://planetcalc.ru/7718/

Z = (x-α)* (x- α ^2)*(x- α ^4)*(x- α ^8) =

X^4 + x^3*( α ^8+ α ^4+ α ^2+ α) + x^2 * (α ^12+ α ^10+ α ^9+ α ^6+ α ^5+ α ^3) + x*( α ^14+ α ^12+ α ^11+ α ^7) + α ^15 = x^4 + x + 1

α ^8+ α ^4+ α ^2+ α mod p(x) = 2* α ^2 + 2* α

α ^14+ α ^12+ α ^11+ α ^7 mod p(x) = -2*3*x^3 – 4*x^2 + 2*x + 3 = 1

Рассмотрим проверочную матрицу Хэмминга (7,4):

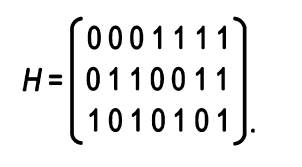
1011

1*x^3+ 0*x^2+ 1*x +1 – кодовый полином

с = (сn-1, cn-2,…, c1,c0)

сдвиг на 1 разряд налево:

с’ = (сn-2, cn-3,…, c0,cn-1)

c(x) = сn-1*x^(n-1)+ cn-2*x^(n-2)+ …+ c1*x + c0

c’(x) = сn-2*x^(n-1)+ cn-3*x^(n-2)+ …+ c0*x + cn-1

c(x)*x = сn-1*x^(n)+ cn-2*x^(n-1)+ …+ c0*x

c’(x) = c(x)*x - сn-1*x^(n) + + cn-1 = c(x)*x – cn-1(x^(n) -1)

c’(x) = c(x)*x mod x^(n) -1

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.