Задача 2.. Задача 3.

Задача 2.

Сколько существует двузначных чисел?

Решение. При образовании чисел используются десять цифр: 0, I, 2, ..., 9. Так как число двузначное, то число десятков может принимать одно из девяти значений: 1,2,3, ..., 9. Число единиц принимает те же значения, и еще 0 (10 вариантов).

Если цифра десятков 1, то цифра единиц может быть любой из десяти: 0, 1,2, ..., 9. Если цифра десятков 2, то цифра единиц вновь может быть любой из десяти: 0, 1, 2, ..., 9, и т. д. Тогда получаем, что возможно 9 • 10 = 90 вариантов (чисел). Разумеется, их легко выписать: 10, 11, 12, ..., 99.

Задача 3.

Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?

Очевидно, что на первом (соответственно, и на последнем) месте может стоять любая цифра (кроме нуля) - 9 вариантов. На втором (соответственно и на предпоследнем) месте может стоять любая цифра - 10 вариантов. На третьем месте (в середине) также может стоять любая цифра - 10 вариантов. Тогда получаем, что возможно 9 • 10 • 10 = 900 вариантов (чисел).

Задача 4. Сколько различных двузначных чисел можно записать с помощью цифр 0, 1, 2, 3?

Решение. В качестве первой цифры может быть выбрана любая из цифр 1, 2, 3 (m=3). Второй цифрой может быть выбрана любая из 4 данных цифр 0, 1, 2, 3 (k=4). Согласно правилу произведения число всевозможных двузначных чисел, составленных с помощью предложенных цифр, равно m k=3 .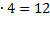

Задача 5. В спортивных соревнованиях участвуют 10 команд. Сколькими способами могут быть распределены золотая, серебряная и бронзовые медали, если любая команда может получить только одну медаль?

Решение. Начнем распределять медали с наименее ценной. Бронзовую медаль может получить одна из 10 команд (10 вариантов). После этого серебряную медаль получит одна из оставшихся 9 команд (9 вариантов). Наконец, золотую медаль получает одна из оставшихся 8 команд (8 вариантов). Следовательно, общее число способов, которыми могут быть распределены золотая, серебряная и бронзовая медали, равно 10 9 8 = 720.

Решить задачи.

№1. Сколько различных двузначных чисел с разными цифрами можно записать, используя цифры:

1) 1. 2 и 3; 2) 0, 3, 5 и 7; 3) 5, 6, 7 и 8?

№2. Сколько различных трехзначных чисел можно записать с помощью цифр:

1) 2 и 3; 2) 0 и 2?

№3. Сколько различных трехзначных чисел, не имеющих одинаковых цифр, можно записать с помощью цифр:

1) 3, 4 и 5; 2) 1, 2, 3 и 4?

⇐ Предыдущая 12