Задача 1.. Задача 2.

Задача 1.

В основания прямой призмы АВСА₁В₁С₁ лежит прямоугольный треугольник АВС с прямым углом С.Через сторону ВС и вершину А₁ проведена плоскость так, что угол ВА₁С равен 30 градусов, А₁В равна 10, АС равна 5.Найти площадь боковой поверхности призмы.

Решение:

Прежде чем приступить к решению задачи необходимо провести её краткий анализ:

площадь боковой поверхности прямой призмы равна произведению высоты призмы на периметр её основания,а это стороны: АС, ВС, АВ и высота АА₁.Из условия известна длина только отрезка АС, поэтому прежде чем приступить к решению задачи, необходимо определить недостающие данные, а это ВС, АВ и АА₁.

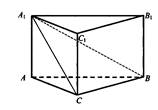
Дано: АВСА₁В₁С₁-прямая треугольная призма,

<С=90⁰, <ВА₁ С=30⁰, А₁В=10, АС=5.

Найти:S_бок

Решение:

1.А₁С┴ВС(по т.т.п.)→Δ А₁ВС-прямоугольный.

2.ВС=1/2А₁В=5(катет лежащий против угла 30⁰).

3.ΔАВС-прямоугольный, по теореме Пифагора:

АВ=√ВС²+АС²=√5²+5²=√50=5√2

4.Δ. А₁АВ-прямоугольный, по теореме Пифагора:

АА₁=√А₁В²-АВ²=√100-50=5√2

5. S_бок=АА₁(АВ+ВС+АС)=5√2(5√2+5+5)=50+50√2

=50(1+√2)

Ответ: S_бок=50(1+√2)

Задача 2.

Диагональ правильной прямоугольной призмы наклонена к плоскости основания под углом 60 градусов. Найти площадь сечения, проходящего через противолежащую сторону верхнего основания и через сторону нижнего основания, если известно, что диагональ основания равна 4√2 см.

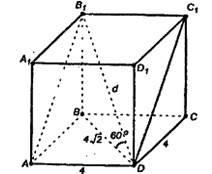
Дано: АВСDА₁ В₁ С₁ D₁-правильная прямоугольная призма, <ВDВ₁=60⁰, ВD=4√2см

Найти:S_AB₁_C₁_D

Решение:

1.AB┴AD, B₁ B┴AD→AB₁┴AD(по т.т.п.)

В₁С₁ ║AD→AB₁┴B₁C_1,AB₁ C₁ D-прямоугольник.

2. d=В₁ D =АС₁.

3.ABCD-квадрат, ВD-биссектриса→< ABD=45⁰

Δ ABD-прямоугольный, АВ=ВD*sin 45⁰=4√2* 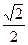=4см, АВ=АD=4 см

4. ВВ₁ =tg 60⁰*BD=√3*4√2=4√6 cм

5.BD=DC₁, ΔDCC₁-прямоугольный, по теореме Пифагора:

DС₁=√DС²+DС₁²=√4²+(4√6)²=√16+16*6=√16(1+6)=4√7см

6.S_AB₁_C₁_D=АD*DС₁=4*4√7=16√7 см

Ответ: S_AB₁_C₁_D=16√7 см

Домашнее задание:

1. С. 67, №219

2. Задача. Дана правильная четырехугольная призма, диагональ которой равна 15, а диагональ основания равна 10√2. Найдите площадь полной поверхности призмы.

⇐ Предыдущая 12