Хелпикс

Главная

Контакты

Случайная статья



Группа 1С-46/ТЭ-49. Тема. Призма.

Стр 1 из 2Следующая ⇒


Группа 1С-46/ТЭ-49

Тема. Призма.

Задание:

1. Изучить теоретические сведения.

2. Написать конспект.

3. Записать примеры выполненных заданий.

4. Выполнить задания.

5. Выполненные задания сфотографировать и отправить на электронную почту tryufelka83@mail.ru или в ЛС социальной сети VKontakte.

6. Выполненные задания сдать до: 27.05

 

Учебник: Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2014.

 Ссылка на учебник онлайн:

https://vpr-klass.com/uchebniki/matematika/atanasyan_10-11kl.html

 

       С. 63-67

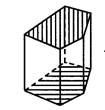Представим два равных между собой многоугольника, которые расположены в параллельных плоскостях и соединим соответственные вершины этих многоугольников. Видно, что получившиеся отрезки параллельны, а каждый из образовавшихся четырёхугольников является параллелограммом, так как имеют попарно параллельные противоположные стороны. Представим два равных между собой многоугольника, которые расположены в параллельных плоскостях и соединим соответственные вершины этих многоугольников. Видно, что получившиеся отрезки параллельны, а каждый из образовавшихся четырёхугольников является параллелограммом, так как имеют попарно параллельные противоположные стороны.

Такой многогранник, составленный из параллелограммов и двух равных многоугольников, расположенных в параллельных плоскостях называется призмой.

Равные многоугольники называют основаниями, а параллелограммы – боковыми гранями.

Отрезки, соединяющие соответственные вершины это боковые рёбра.

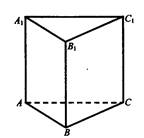Если в основании призмы лежит треугольник, то призма называется треугольной.

Высотой призмы называется перпендикуляр, проведённый из любой точки основания к плоскости другого. Такой многогранник, составленный из параллелограммов и двух равных многоугольников, расположенных в параллельных плоскостях называется призмой.

Равные многоугольники называют основаниями, а параллелограммы – боковыми гранями.

Отрезки, соединяющие соответственные вершины это боковые рёбра.

Если в основании призмы лежит треугольник, то призма называется треугольной.

Высотой призмы называется перпендикуляр, проведённый из любой точки основания к плоскости другого.

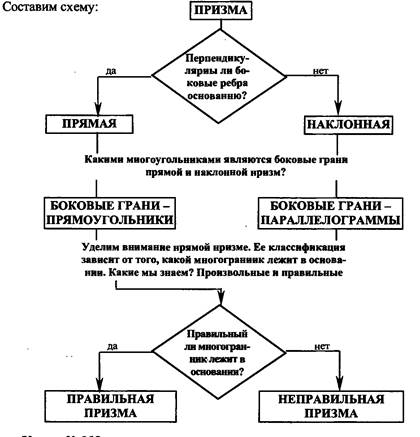
В случае, если боковые рёбра не перпендикулярны основаниям, то призма называется наклонной. В противоположном случае-прямой, в такой призме боковые рёбра будут одновременно и высотами.

Боковые гранипрямой призмы являются прямоугольниками.

Боковые грани наклонной призмы являются параллелограммами.

Если в основании призмы лежит правильный многоугольник (стороны и углы равны), то призма называется правильной, в противном случае- неправильной.

 

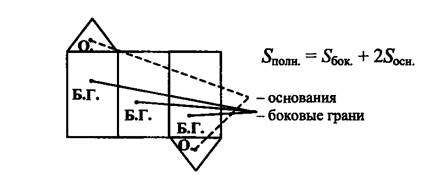
Сумма площадей всех граней призмы называется площадью полной поверхности.

Сумма площадей только боковых граней призмы называется площадью боковой поверхности.

Несложно выяснить, что площадь полной поверхности равна сумме площадей боковой поверхности и площади оснований.

 

Боковыми гранями прямой призмы являются прямоугольники, поэтому площадь боковой поверхности равна сумме площадей этих прямоугольников.

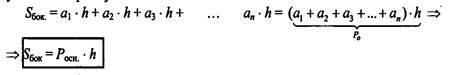Площадь боковой поверхности прямой призмы равна произведению высоты призмы на периметр её основания.

 

 


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.