Задача №1

Урок 121 Дата 15.06.20,

Тема Применение производной и интегралов к решению практических задач

1. Укажите неверное равенство:

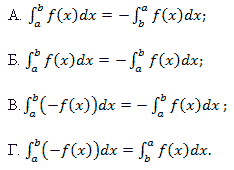
2 Вычислите интеграл:

2. “Смысл” площади криволинейной трапеции - неоднозначен. В зависимости от рассматриваемого явления площадь криволинейной трапеции может выражать различные физические, химические, биологические явления. Математический анализ является средством изучения функции, то тогда и средством изучения окружающих нас явлений. Наглядными примерами применения свойства непрерывности функции могут служить различные законы движения тела S=f(t), выражающие зависимость пути S, пройденного телом, от времени t. Время и пространство непрерывны, при этом тот или иной закон движения S=f(t) устанавливает между ними непрерывную связь: малому приращению времени соответствует малое приращение пути. В дифференциальном исчислении, основоположниками которого были И.Ньютон и Лейбница, существует две задачи:

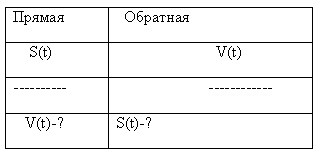
Задача №1

Пусть скорость заданная функцией времени, точки движущейся по оси ОХ имеет вид V=f(t).Найти закон движения х(t)=х.

Решение: Закон движения зададим формулой х =G(t) . Известно, что х` =f(t), где f(t)- непрерывная функция, тогда G`(t)=f(t) – уравнение в котором производная неизвестна (такие уравнения называются дифференциальными).

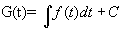(где C находится из дополнительного условия задачи, например при t=0).

12 Следующая ⇒