VIII. Первичное закрепление.(5мин)

Стр 1 из 2Следующая ⇒

Урок119-121

Тема: ,,Взаимное расположение сферы и плоскости. Касательная плоскость к сфере.”

Урок обобщения и систематизации

Цели урока:

Ход урока:

«Знание – самое превосходное из владений. Все стремятся к нему, само же оно

не приходит».

Тестовая работа по теме «Сфера и шар».

Решение

Найдите координаты центра О и радиус сферы R, заданной уравнением

(х-2)²+(у+3)²+z² = 25.

Напишите уравнение сферы радиуса R с центром в точке O, если O(2;0; -1),

R = 7.

Проверьте лежит ли точка А на сфере, заданной уравнением

(х+2)²+(у-1)²+(z-3)² = 1,

если А(-2;1; 4).

Докажите, что данное уравнение

х²+у²+z² +2х -2у = 2 является уравнением сферы, запишите координаты центра O и радиус сферы R.

Учебник Геометрия10-11 клас Л.С. Атанасян и другие

Рассмотрим задачу

№ 586.Отрезок ОН-высота тетраэдра ОАВС. Выясните взаимное расположение сферы радиуса R с центром О и плоскости АВС, если:

а) R=6 дм, ОН=60 см;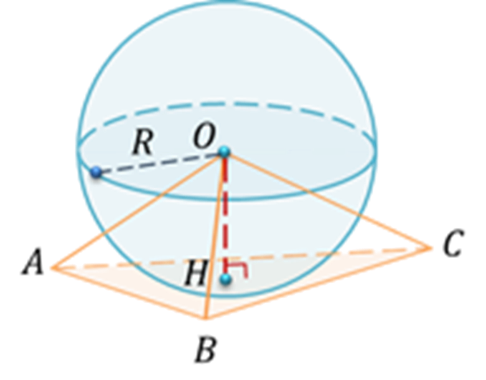

б) R=3 м, ОН=95 см;

в) R=5 дм, ОН=45 см;

г) R=3,5 дм, ОН=40 см;

Анализируя условие задачи обучающиеся делают вывод, что знаний, полученных на прошлом уроке недостаточно для решения поставленной проблемы. Чтобы решить задачу необходимо установить зависимость взаимного расположения сферы и плоскости АВС от длин радиуса R и высоты тетраэдра ОН.

Обучающиеся формулируют тему, цели и задачу урока:

Цели:

изучить виды взаимного расположения сферы и плоскости;

сформировать навыки решения задач.

Задача: провести исследование взаимного расположения сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от ее центра до плоскости.

1 На этом уроке мы должны изучить возможные случаи взаимного расположения сферы и плоскости в пространстве.

Прежде чем приступить к новой теме, давайте вспомним некоторые факты.

В курсе планиметрии мы с вами рассматривали три случая взаимного расположения прямой и окружности, в зависимости от соотношения расстояния от центра окружности до прямой и радиуса окружности. Повторим их:

1) Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

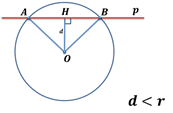
2) Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.

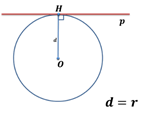
3) Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

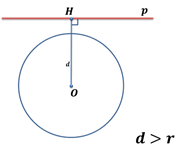
В стереометрии же можно рассмотреть взаимное расположение сферы и плоскости в пространстве.

Итак, давайте исследуем взаимное расположение сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от ее центра до плоскости.

Для этого введём следующие обозначения. Обозначим радиус сферы буквой 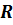, центр сферы буквой 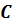, а расстояние от её центра до некоторой плоскости альфа – буквой .

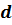Введём систему координат 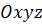. Затем построим плоскость 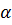, совпадающую с плоскостью .

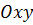Изобразим сферу с центром в точке 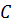, лежащей на положительной полуоси .

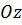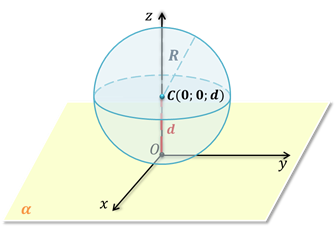
Обратите внимание, в этой системе координат точка 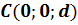, где 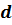– расстояние (перпендикуляр) от центра сферы до плоскости .

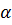В зависимости от соотношения 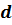– расстояния от центра сферы до плоскост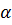и и 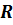– радиуса сферы возможны три случая взаимного расположения сферы и плоскости в пространстве.

1. d<R

Если расстояние от центра сферы до плоскости меньше радиуса сферы, то …

2. d=R

Если расстояние от центра сферы до плоскости равно радиусу сферы, то …

3. d>R

Если расстояние от центра сферы до плоскости больше радиуса сферы, то …

Ваша задача исследовать каждый случай, сделать соответствующие выводы и проиллюстрировать при помощи набора прозрачных геометрических тел с сечениями.

1 ряд исследует 1 случай, 2 ряд -2 случай и 3 ряд-3 случай.

Работа проводится в парах.

VI. Реализация построенного проекта. (15 мин)

Рассмотрим первый случай. Если .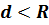

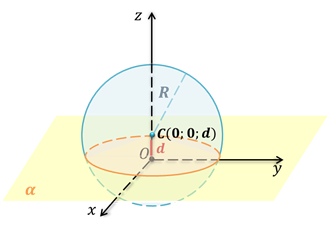
Если расстояние от центра сферы до плоскости меньше радиуса сферы, то в данном случае сфера и плоскость пересекаются по окружности.

Сделаем вывод. Если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность.

Понятно, что сечение шара плоскостью есть круг. С приближением секущей плоскости к центру шара радиус сечения (круга) увеличивается.

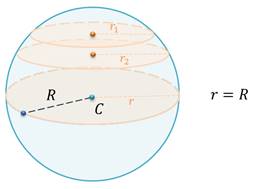
Тогда расстояние от центра сферы до секущей плоскости равно нулю, а в сечении получается круг, радиус которого равен радиусу шара.

Определение:

Плоскость, проходящая через диаметр шара, называется диаметральной.

А круг, полученный в результате сечения, называется большим кругом шара.

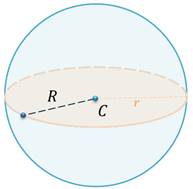
Если же секущая плоскость не проходит через центр шара, то очевидно, что тогда радиус сечения будет меньше радиуса сферы.

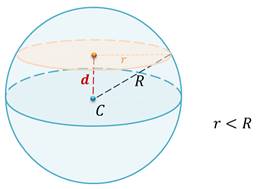
Рассмотрим второй случай. Если .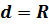

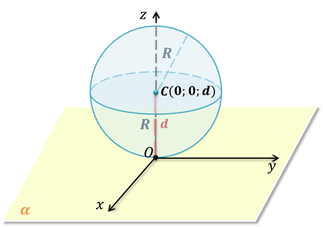
Если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку.

Плоскость, имеющая со сферой одну общую точку, называется касательной плоскостью к сфере, а их общая

точка – точкой касания.

Свойство касательной функции:

И рассмотрим третий случай. Если .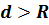

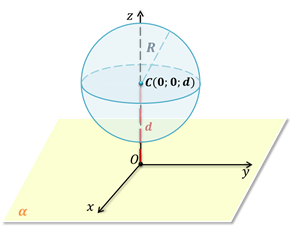
Если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек.

VIII. Первичное закрепление.(5мин)

Вернемся к задаче № 586.

Применим к её решению приобретённые знания и сделаем выводы.

а) R=6 дм, ОН=60 см;

в) R=5 дм, ОН=45 см;

г) R=3,5 дм, ОН=40 см;

Решение: чтобы выяснить взаимное расположение сферы и плоскости, мы должны рассмотреть соотношение расстояния от центра сферы до плоскости и радиус сферы.

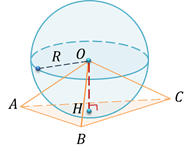
В первом пункте, расстояние от центра сферы до плоскости равно радиусу сферы.

а) R=6 дм=60 см, ОН=d=60 см =>d = R.

А это говорит о том, что сфера и плоскость имеют только одну общую точку или иначе говоря, плоскость касается сферы.

Во втором пункте, расстояние от центра сферы до плоскости меньше радиуса сферы.

в) R=5 дм=50 см, ОН=d=45 см =>d < R.

Значит, сфера и плоскость пересекаются по окружности.

И в последнем пункте, расстояние от центра сферы до плоскости больше радиуса сферы.

г) R=3,5 дм=35 см, ОН=d=40 см =>d > R.

Следовательно, сфера и плоскость не имеют общих точек, и значит, не пересекаются.

12 Следующая ⇒