
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ. Уроки Задачи на подсчет числа размещений, перестановок, сочетаний. Повторить. Изучение нового. Перестановки. В этой задаче было найдено число всевозможных соединений (комбинаций) из четырех элементов, которые отличались одно от д
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
Уроки Задачи на подсчет числа размещений, перестановок, сочетаний
Цели: изучить понятия: факториал, размещения, перестановки, сочетания; формирование навыков решения задач на подсчет числа размещений, перестановок, сочетаний.
Повторить
1. Принцип сложения
2. Принцип умножения
3. Натуральные числа
Изучение нового
1. Факториал – произведение первых n натуральных чисел
Обозначается: n!=1 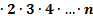 0!=1 1!=1
0!=1 1!=1
Вычислить: 1) 2! 2) 3! 3)4! 4) 5!
Упростить: 1) 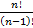 2)
2) 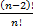 3)
3) 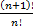
2. Перестановки
Задача 1. Сколькими способами можно поставить рядом на полке 4 различные книги?
Решение. На первое место можно поставить любую из 4 книг, на второе – любую из трех оставшихся, на третье – любую из двух оставшихся и на четвертое место – последнюю оставшуюся книгу. Применяя последовательно правило произведения, получим
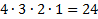 .
.
 . Книги можно поставить 24 способами
. Книги можно поставить 24 способами 
В этой задаче было найдено число всевозможных соединений (комбинаций) из четырех элементов, которые отличались одно от другого порядком расположения этих элементов. Такие соединения называются перестановками.
Определение. Перестановками из n элементов называются соединения, которые состоят из одних и тех же n элементов и отличаются одно от другого только порядком их расположения.
Отличительной особенностью перестановок является то, что в каждой из них участвуетВСЁмножество, то есть, все  объектов.
объектов.
Обозначают 
Формула числа перестановок 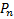 из n различных элементов:
из n различных элементов: 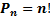
Задача 2. Сколькими способами можно положить 6 различных открыток в 6 имеющихся конвертов (по одной открытке в конверт)
Решение. 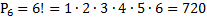
Задача 3: Сколькими способами можно переставить яблоко / банан / груша ?
Решение. 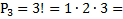 6
6
Вопрос второй: Сколькими способами можно выбрать а) один фрукт, б) два фрукта, в) три фрукта
Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан.
б) Перечислим все возможные сочетания двух фруктов:
яблоко и груша;
яблоко и банан;
груша и банан.
И, наконец, три фрукта можно выбрать единственным способом:
Выборки отличались друг от друга только составом. Такие соединения называют сочетаниями.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|