Главная Контакты Случайная статья Автоматизация Антропология Археология Архитектура Биология Ботаника Бухгалтерия Военная наука Генетика География Геология Демография Деревообработка Журналистика Зоология Изобретательство Информатика Искусство История Кинематография Компьютеризация Косметика Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Материаловедение Медицина Менеджмент Металлургия Метрология Механика Музыка Науковедение Образование Охрана Труда Педагогика Полиграфия Политология Право Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Электротехника Энергетика
	II Вариант. Пример 2. Стр 1 из 2Следующая ⇒   Тема: Использование свойств и графиков функций для решения уравнений и неравенств Цель работы: - применить умения по владению стандартными приемами решения уравнений и систем. Задание: I Вариант II Вариант
1. Решите неравенство графически
−x2+6x−5≥0		−x2+6x−9<0
2. Решите графически систему уравнений.
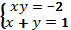
3. Решить графически уравнение.

Порядок выполнения:

1. Внимательно прочитать тему и цель практической работы.

2. Изучить учебный материал по теме.

3. Ответить на вопросы.

4. Выполнить задания.

5. Подготовить отчет.

Пояснения к работе (учебный материал):

Если графики функций пересекаются в одной точке, то уравнение имеет один корень, если в двух, то два решения.

Если графики не пересекаются, то уравнение не имеет корней.

Первый способ графического решения квадратного уравнения заключается в построении параболы y=ax² + bx + c и нахождении корней уравнения ax²+bx+c=0 как абсцисс точек пересечения параболы с осью Оx.

Если парабола пересекает ось Оx в двух точках, то соответствующее уравнение имеет два действительных корня;

если парабола касается оси Оx, то уравнение имеет два равных действительных корня;

наконец, если парабола не пересекает Ось Оx, то уравнение не имеет действительных корней.

Второй способ графического решения квадратного уравнения заключается в том, что уравнение в виде

При выполнении практической работы рассмотрите следующие примеры:

Пример 1.

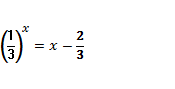
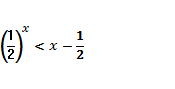
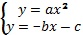
Выяснить с помощью графиков, сколько корней имеет уравнение 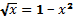/ Найти приближённое значение этих корней.

Решение: Построим на одном рисунке , используя свойства этих функций.

Графики пересекаются в одной точке (≈0,5; ≈0,75)

Ответ: x≈0.5.

Пример 2.

 Решите неравенство

Решение. Неравенство удобно решить графически.

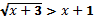
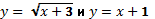Построим на одном чертеже графики функций , используя свойства функций.

Ответ: -3 ≤ x < 1