События называются равновозможными, если условия испытания обеспечивают одинаковую возможность осуществления каждого из них.

Пример 1. В ящике имеются стандартные и нестандартные детали. Наудачу берут одну деталь. События А1 — «появилась стандартная деталь» и А2 — «появилась нестандартная деталь» являются несовместными событиями.

Пример 2. Брошена игральная кость. Событие А1 — «появление двух очков» и событие А2 — «появление четного числа очков» совместны, так как появление одного из них не исключает появление другого.

' ПрймерЗ. Появление того или иного числа очков при бросании игральной кости есть события равновозможные, так как игральная кость изготовляется из однородного материалу и имеет строго симметричную форму.

Пример 4. Появление герба и появление цифры при бросании симметричной монеты есть события равновозможные.

События 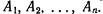образуют полную группу событий, если в результате данного испытания непременно произойдет хотя бы одно из них.

Пример 3 : В урне имеются три белых шара, перенумерованных цифрами 1, 2, 3, и пять черных шаров, перенумерованных цифрами 1, 2, 3, 4, 5. Из урны наугад берут один шар. События:

А₁ — «появление шара с цифрой 1»,

А₂ — «появление шара с цифрой 2»,

А₃ — «появление шара с цифрой 3»,

А₄ — «появление шара с цифрой 4»,

А₅ — «появление шара с цифрой 5» образуют полную группу.

Важную роль играет полная группа несовместимых событий, т. е. такая группа событий, что в результате данного испытания непременно произойдет только одно событие данной группы.

Пр и м е р№6. ~ При бросаний игральной кости возможны события:

А₁— «появление одного очка»,

А₂ — «появление двух очков»,

А₃ — «появление трех очков»,

А₄ —«появление четырех очков»,

А₅ — «появление пяти очков»,

А₆— «появление шести очков».

Эти события образуют полную группу несовместных событий.

Два случайных события называются противоположными, если одно из них происходит в том и только том случае, когда не происходит другое.

Событие противоположное событию А обозначают Ä и читают (не А)

Пример 7. Попадание и промах при выстреле по мишени противоположные события. Если А — попадание, то Ä — промах.

Пример 8. Появление четного числа очков при бросании игральной кости — событие, противоположное появлению нечетного числа очков.

Очевидно, что противоположные события образуют полную группу событий.

Операции над событиями .

Прежде всего установим некоторые отношения между событиями. Рассмотрим события:

А — «появление трех очков при бросании игральной кости»,

В —«появление нечетного числа очков при бросании игральной кости».

Очевидно, что если произошло событие А, то непременно произошло и событие В. В этом случае говорят «А влечет за собой В» (или «В является следствием А») и записывают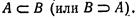

Если события А и В таковы, что 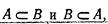то они называются равными (равносильными), при этом пишут А=В.

Пример 1. Брошена симметричная монета. Событие А— «появление герба», событие В — «непоявление цифры». Очевидно, что 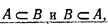и, следовательно, А = В.

Определение : Суммой или объединением двух событий А и В называют событие С состоящее в осуществлении хотя бы одного события А или В (безразлично, какого именно, или обоих, если это возможно).

Символически записывают так: С = А+В

Суммой или объединением нескольких событий 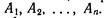называется событие С, состоящее в осуществлении хотя бы одного из событий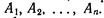

Пример 3. Найти сумму событий: А — «появление одного очка при бросании игральной кости» и В — «появление двух очков при бросании игральной кости». Суммой А + В является событие С—«появление не больше двух очков при бросании игральной кости», поэтому : А+В=С

Если события А и В — несовместные, то сумма А + В является событием, состоящим в осуществлении одного из этих событий, безразлично какого (их

совместное осуществление невозможно).

Непосредственно из определения суммы событий вытекают следующие свойства сложения:

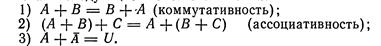
Умножение

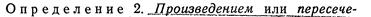Ли В называется соб

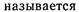
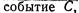состоящее в одновременном осуществлении А и В

Символически произведение записывают так:

С = АВ или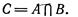

Теоретико - множественная интерпретация произведения событий дана на рис. 119.

Рис. 119. Произведением или пере-

сечением нескольких событий 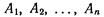называется событие С, состоящее в одновременной осуществлении всех событий 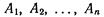Символически:

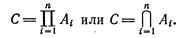
Например 4? Найти произведение событий А — «студенту попался экзаменационный билет с четным номером» и В — «студенту попался экзаменационный билет с номером, кратным пяти».

Решение. Произведением АВ является событие

С — «студенту попался экзаменационный билет с номером, кратным десяти», поэтому АВ = С

Если события А и В— несовместные, то АВ = V, т. е.. произведение А В — невозможное событие.

Можно показать, что для умножения событий имеют место свойства:

1) АВ = В А (коммутативность);

2) А (ВС) = (АВ)С (ассоциативность);

3) А (В + С) = АВ + АС (дистрибутивность);

4) AA=V.

Формула полной вероятности.

Операции над вероятностями представляют собой правила, служащие для вычисления вероятностей случайных событий через вероятности элементарных событий. При решении многих задач оказывается полезным одно следствие из этих правил, известное под названием формулы полной вероятности. Пусть событие А может произойти только с одним из событий Н₁, Н₂, …Н_n, образующих полную группу несовместных равновозможных событий. Тогда вероятность события F вычисляется по формуле полной

вероятности: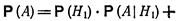

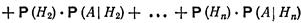
Пример 1. В учебных мастерских на станках a, b и с изготовляют соответственно 25, 35 и 40% всех деталей. В их продукции брак составляет соответственно 15, 12 и 6%. Найти вероятность того, что наугад взятая деталь дефектна.

Решение. Обозначим события:

А — «наугад взятая деталь дефектна»,

Н₁ — «деталь изготовлена на станке а»,

Н₂— «деталь изготовлена на станке 6»,

Н₃ — «деталь изготовлена на станке с».

Очевидно, что события Н₁ Н₂, Н₃ образуют полную группу и P(Н₁) = 0,25, Р(Н₂) = 0,35, Р(Н₃)=б,4. Кроме того, числа 0,15; 0,12; 0,06 (15%, 12% и 6%) являются условными вероятностями события А при выполнении событий (гипотез) Н₁ Н₂, Н₃ соответственно, т. е.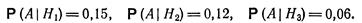

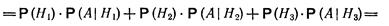
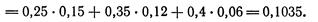
Математическая статистика и ее роль в медицине и здравоохранении.

В самых различных областях производственной и научной деятельности приходится проводить изучение (обследование, измерение, проверку) объектов, принадлежащих некоторой совокупности по какому-либо признаку. Иногда приходится исследовать каждый объект совокупности, т.е. проводить сплошное исследование. Но во многих других случаях в силу различных причин исследовать каждый объект невозможно.

Поэтому на практике гораздо чаще применяется выборочное исследование. При выборочном исследовании из всей совокупности отбирают некоторым образом определенное число объектов и только их подвергают исследованию.

Совокупность всех исследуемых объектов называют генеральной совокупностью.

Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов из генеральной совокупности.

Под случайным отбором при образовании выборки понимают такой отбор, при которой все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку.

Выборка может проводиться двумя способами

- При первом объект извлекается из генеральной совокупности, исследуется, возвращается в исходную генеральную совокупность, затем снова извлекается некоторый объект, исследуется и возвращается в генеральную совокупность и т.д. Полученную выборку называют повторной.

- При втором способе после исследования объекты в генеральную совокупность не возвращаются. Выборку называют бесповторной.

Таким образом, при бесповторной выборке каждый объект исследуется только один раз, при повторной выборке один и тот же объект может подвергаться несколько раз.

Число объектов выборочной или генеральной совокупности называют объемом выборки

Например, если из 10,000 изделий для контроля отобрано 100 изделий, то объем генеральной совокупности N=10,000, а объем выборки n=100.

Математическая статистика занимается вопросом: можно ли установить какое-либо свойство выборки, считать, что это свойство с определенной вероятностью присуще всей генеральной совокупности?

Чтобы по выборке можно было судить обо всей генеральной совокупности выборка должна:

- достаточно полно отражать изучаемое свойство объектов совокупности;

- достаточно представительной (репрезентативной); - отбор объектов в выборку осуществляется действительно случайно.

- изучаемому свойству должна быть присуща статистическая устойчивость: при многократном повторении исследования должна иметь место статистическая устойчивость частот наблюдаемых событий.

Для статистической обработки результат исследования объектов, составляющих выборку, представляют в виде числовой выборки, т.е. в виде последовательности чисел Х₁, Х_2, … X_n.

Разность между наибольшим значением числовой выборке и ее наименьшим значением называют размахом выборки. Выборку, представляющую собой неубывающую последовательность называют вариационным рядом.

Любую числовую выборку можно записать в виде вариационного ряда.

Например, выборку 1,10,-2,1,0,1,10,7,-2,10,10,7 запишем в виде неубывающей последовательности, получим вариационный ряд

-2, -2, 0, 1, 1, 1, 7, 7, 10, 10, 10, 10.

Размах выборки равен 10-(-2)=12.

Пусть при исследовании некоторой генеральной совокупности получена числовая выборка объема n, причем значение Х₁ встречается в выборке n₁ раз, значение Х₂-n₂ раз, …, X_k-n_k раз.

Числа n₁, n₂, n₃, …, n_k называют частотами, а их отношение к объему выборки, т.е. 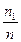; ; …; - относительными частотами соответствующих значений Х₁; Х₂; …; Х_k выборки.

Сумма частот равна объему выборки, а сумма относительных частот равна единице, т.е.,

n₁+n₂+...+n_k=n

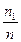+ +…+ =1

Последовательность пар (Х₁, n₁,),( Х_2, n₂,),… (Х_k_, n_k) называют статистическим рядом.

Обычно статистический ряд записывают в виде таблицы.

Х₁	Х₂	Х₃	Х₄	…	Хi	…	X_k
n₁	n₂	n₃	n₄	…	ni	…	n_k

Или

Х₁	Х₂	Х₃	…	Хi	…	X_k
n₁/n	n₂/n	n₃/n	…	ni/n	…	n_k/n

Пример: Для выборки 3,8,-1,3,0,5,3,-1,3,5 определить объем и размах. Записать выборку в виде вариационного ряда и в виде статистического ряда. Найти выборочное распределение.

Решение: объем выборки n=10, ее размах 8-(-1)=9, записав ее в виде вариационного ряда получим : -1,-1,0,3,3,3,3,5,5,8 в виде статистического ряда (-1,2); (0,1); (3,4);(5,2);(8,1); или в виде таблицы

-1

Для контроля находим сумму частот: 2+1+4+2+1=10

Вычислив относительные частоты найдем выборочное распределение

-1
2/10	1/10	4/10	2/10	1/10

Для контроля убедимся в том, что сумма относительных частот равна 1

2/10 + 1/10 + 4/10 + 2/10 + 1/10 = 1

Графическое изображение выборки :

Полигон и гистограмма.

Для наглядного представления о выборке часто пользуются различными графическими изображениями. Простейшими изображениями выборки являются полигон и гистограмма.

Пусть выборка задана статистическим рядом ( Х₁, n₁), ( Х₂, n₂),…, (X_n, n_k)

Полигоном – частот называют ломанную с вершинами в точках ( Х₁, n₁), ( Х₂, n₂),…, (X_n, n_k)

Полигоном относительных частот называют ломанную с вершинами в точках (Х₁, n₁/n), (Х₂, n₂/n),…,( X_k , n_k/n)

Полигон относительных частот получается из полигона частот путем сжатия в n раз, где n – объем выборки.

При большом объеме выборки более наглядное представление о ней дает гистограмма. Для ее построения промежуток от наименьшего значения выборки до наибольшего ее значения разбивают на несколько частотных промежутков длинны h. Для каждого частичного промежутка подсчитывают сумму S_i частот значений выборки, попавших в этот промежуток. Значение X_i выборки, совпадавшее с правым концом промежутка, относят к следующему промежутку (если X_i – не наибольшее значение выборки). Затем на каждом частичном промежутке, как на основании, строим прямоугольник с высотой S_i/n. Объединением всех построиных таким образом прямоугольников называют гистрограммой частот.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которого являются частичные промежутки длинны h, а высотами – отрезки длины S_i/n, где S_i - сумма частот значений выборки, попавших в i – й промежуток.

Из определения гистограммы ясно, что ее площадь равна объему выборки. В практических задачах в зависимости от объема выборки в большинстве случаев целесообразно брать 10-20 частичных промежутков.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные промежутки – отрезки длины W_i/h, где W_i – сумма относительных частот значений выборки, попавших в i – й промежуток.

Площадь относительных частот гистограммы равна единицы

Пример: В результате измерения напряжения (в вольтах) в электросети получилась выборка

218 221 215 225 225 217

224 220 220 219 221 219

222 227 218 220 223 230

223 216 224 227 220 222

Построить гистограмму частот, если число частичных промежутков – 5.

Решение

Наименьшее значение выборки – 215, наибольшее – 230. Находим длину частичных промежутков h=(230-215)/5, h=3. подсчитываем с учетом крайности число

[215; 218] – 3,

[218; 221) – 8,

[221; 224) – 6,

[224; 227) – 5,

[227; 236) – 2,

Высоты прямоугольников: (1; 8/3; 2; 5/3; 2/3)

Контроль: площадь равна объему выборки

3*(1+8/3+2+5/3+2/3)=24.

Методы обработки статистических данных

Математическая статистика — это раздел математики, который изучает методы обработки и классификации статистических данных для получения научно обоснованных выводов и принятия решений. Примером статистических данных служит последовательность значений случайной величины, полученных в результате некоторого наблюдения, эксперимента

(опыта). Так, последовательность чисел, которые получаются в результате неоднократного измерения некоторой величины, скажем, взвешивания некоторого тела на аналитических весах, является простейшим примером статистических данных. Рассмотрим еще один пример: электрическая лампочка считается стандартной, если она горит не менее 1400 часов. Каким образом определить, в какой степени партия лампочек, выпущенная заводом, соответствует установленному стандарту? Очевидно, что испытывать все лампочки бессмысленно. Поэтому выбирают случайным образом некоторое количество лампочек для испытания. Последовательность полученных данных о продолжительности горения отобранных лампочек представляет собой статистические данные, которые, будучи обработаны методами математической статистики, позволяют делать выводы о качестве данной партии продукции. В связи с тем, что статистические данные зависят от случайных факторов, математическая статистика тесно связана с теорией вероятностей, которая является ев теоретической основой.

Как мы уже знаем, теория вероятностей устанавливает правила нахождения вероятностей более сложных событий (суммы, произведения событий) и вычисления различных числовых характеристик случайных величин (математического ожидания, дисперсии) по заданным вероятностям исходных событий. На практике же редко встречаются задачи, в которых вероятности рассматриваемых событий были бы заранее известны. В таких случаях методами математической статистики можно получить сведения о случайной величине путем изучения небольшого набора наблюденных значений случайной величины, содержащего как можно больше

нужных сведении о случайной величине.

Основные задачи математической статистики могут быть сформулированы следующим образом:

а) оценка неизвестных параметров случайной величины (вероятности случайного события, математического ожидания случайной величины, дисперсии, функции распределения);

б) статистическая проверка гипотез, т. е. проверка предположений, сделанных относительно некоторых случайных событий, случайных величин (о вероятности события, о законе распределения случайной величины и т. д.);

в) принятие решений (сюда относятся, в частности, задачи оптимального выбора момента настройки или замены действующей аппаратуры, например, определения срока замены двигателя самолета, отдельных деталей станков и т. д.).

В настоящее время математическая статистика продолжает бурно развиваться; при этом все больше расширяется круг ее задач и методов исследования с широким применением ЭВМ. Так, разрабатываются статистические методы распознавания образов, определения характеристик элементов системы автоматического управления и т. д.

Математическая и прикладная статистика используется при планировании и организации производства, при анализе технологических процессов при предупредительном и приемочном контроле качества продукции и в других практических задачах.

Пусть требуется изучить множество значений случайной величины или совокупности объектов относительно некоторого признака. Например, требуется определить процент изделий, выпускаемых одним и тем же оператором, параметры которых отличаются от номинальных. Если число элементов в совокупности не очень большое, обследование объекта не связано с его уничтожением или не требует больших затрат, то можно исследовать каждый элемент в отдельности, фиксировать значение исследуемого признака и соответствующей обработкой результатов сделать тот или иной вывод о наблюдаемом или измеряемом признаке. Если же совокупность состоит из очень большого числа объектов, или исследование связано с уничтожением объекта, или оно дорого стоит, то сплошное обследование невозможно. Невозможно, например, исследовать на долговечность всю партию электрических лампочек, так как в результате исследуемые лампочки сгорают и вся партия уничтожилась бы.

В этих случаях выводы об исследуемом признаке делаются на основе изучения ограниченного числа объектов, должным образом отобранных из общей совокупности. Основными понятиями математической статистики являются генеральная и выборочная совокупности. Множество всех значений некоторой изучаемой величины или, другими словами, совокупность всех объектов, которая подлежит изучению, носит название генеральной совокупности, а специальным образом отобранная группа объектов — выборочной совокупности или выборки. Например, партия всех электрических лампочек, которая подлежит изучению, является генеральной совокупностью, а множество лампочек, взятых для обследования, составляет выборочную совокупность. Число объектов совокупности (генеральной или выборочной) называется объемом данной совокупности (выборки). Например, если цех выпустил 2000 деталей, а для обследования отобрано 150 деталей, то объем генеральной совокупности равен 2000 (N = 2000), а объем выборки— 150 (п = 150).

Сейчас можно сказать, что основная задача математической статистики состоит в получении обоснованных выводов о свойствах генеральной совокупности по известным свойствам извлеченной из нее выборки. Рассмотрим теперь основные виды выборок. Различают выборки с возвращением и без возвращения. Если после фиксирования значения параметра объект возвращается в генеральную совокупность и, таким образом, он может многократно повторяться в выборке, то говорят о выборке с возвращением или с повторением. Если же раз отобранный объект обратно не возвращается и он не может больше, чем один раз, повторяться в выборке, то такая выборка называется выборкой без возвращения или без повторения. Заметим, что когда объем выборки намного меньше объема генеральной совокупности, то различие между выборкой с возвращением и без возвращения практически исчезает. Говорят, что выборка репрезентативна (представительна), если она достаточно «хорошо» представляет изучаемые признаки генеральной совокупности. Важным условием обеспечения репрезентативности выборки является соблюдение случайности отбора, т. е. все объекты генеральной совокупности должны иметь равные вероятности попасть в выборку. С целью обеспечения репрезентативности выборки в зависимости от конкретных условий применяются различные способы отбора: простой, типический, механический, серийный.

· Простым называется отбор, при котором из генеральной совокупности случайным образом извлекается по одному элементу с возвращением или без возвращения. Например, для изучения белых медведей экспедиция ловит- случайным образом попавшихся ей белых медведей, измеряет исследуемые параметры и отпускает на волю или сдает в зоопарк в зависимости от целей, которые стоят перед ней.

· Типическим называется отбор, при котором объекты случайным образом отбираются из каждой «типической» части генеральной совокупности. Например, если детали изготовляются разными цехами, то для обеспечения репрезентативности выборки отбор производится случайным образом с соблюдением пропорций из продукции каждого цеха. Типическим отбором пользуются тогда, когда исследуемый признак существенно колеблется в различных частях генеральной совокупности.

· Механическим называется отбор, при котором объекты отбираются через определенный интервал, скажем, каждый пятый, двадцатый, сотый и т. д. Механическим отбором надо пользоваться осторожно.Например, если резец заменяется после тридцати обработанных деталей, то нельзя составлять выборку, отбирая каждую десятую или пятнадцатую детали. Отметим, что втакихслучая хцелесообразно, чтобы номер отбираемой детали

и период ритма работы были взаимно простыми числами. Тогда в выборку попадут объекты со всех точек периода ритма.

· Серийным называется отбор, при котором выборка состоит из целой серии объектов. Этим способом пользуются в тех случаях, когда исследуемый признак в генеральной совокупности колеблется незначительно.

Например, если квалификация всех рабочих цеха, качество технических средств и сырья1 существенно не изменяются в течение недели, то для проверки недельной продукции данного цеха можно провести сплошную проверку продукции одного дня.

На практике для обеспечения репрезентативности выборки пользуются сочетанием вышеуказанных способов отбора. Если отбор объектов из генеральной совокупности и образование выборки невозможны непосредственным манипулированием самими объектами ввиду их громоздкости, труднодоступности или по другим причинам, то объектам генеральной совокупности присваиваются номера, которые записываются, например, на отдельных карточках, удобных для перемешивания и осуществления отбора. Путем случайного отбора карточек образуется выборка заданного объема, а впоследствии из генеральной совокупности отбираются те объекты и номера которых совпадают с номерами карточек, попавших в выборку. Описанным способом поступают, например, при составлении тиражей выигрышных билетов в денежно-вещевых лотереях, облигаций трехпроцентного займа и др.

В научных исследованиях для формирования выборок чаще всего пользуются так называемыми таблицами случайных чисел, которые могут быть получены при помощи случайного выбора карточек или специальными алгоритмами на ЭВМ. Существуют таблицы случайных чисел четырехзначные, пятизначные и т. д. Если надо, например, образовать выборку объема и из генеральной совокупности объема N = 100 000, то берем пятизначную таблицу случайных чисел и выписываем любую группу из последовательных ее чисел.

Обследованию подвергаются те объекты генеральной совокупности, номера которых совпадают с выписанными числами из таблицы случайных чисел.

⇐ Предыдущая 12