
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
События . называются несовместными, если осуществление одного из них исключает осуществление других.
Тема: Производная и дифференциал.
2.1 Производная функции по ее аргументу.
Задача 3. Для произвольной функции y = f(x), непрерывной в рассматриваемой области существования, найти аналитическое выражение предела отношения ее приращения к приращению аргумента при стремлении приращения аргумента к нулю для любой точки М(х,у)у.
 Решение: Пусть имеем функцию y = f(x) с графиком, изображенном на рисунке 24. Возьмем на графике заданной функции любую точку М, т.к. она любая, т.е. текущая, то ей будет соответствовать абсцисса, равная аргументу х и ордината у, равная f(x). Дадим аргументу х какое-нибудь приращение х, т.е. получим новый аргумент х + х. Ему будет соответствовать новое значение у(х + х) = f(x + x). Разность между полученным в результате приращения аргумента значением функции f(x + x) и значением функции от аргумента без этого приращения f(x) называется приращением функции — у, т.е.
Решение: Пусть имеем функцию y = f(x) с графиком, изображенном на рисунке 24. Возьмем на графике заданной функции любую точку М, т.к. она любая, т.е. текущая, то ей будет соответствовать абсцисса, равная аргументу х и ордината у, равная f(x). Дадим аргументу х какое-нибудь приращение х, т.е. получим новый аргумент х + х. Ему будет соответствовать новое значение у(х + х) = f(x + x). Разность между полученным в результате приращения аргумента значением функции f(x + x) и значением функции от аргумента без этого приращения f(x) называется приращением функции — у, т.е.
(28)
Теперь решим задачу 3 до конца. С учетом рассуждений в задачах 1 и 2 и равенства (28) получим:
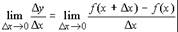 (29)
(29)
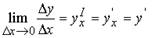 В математике равенство (29) называют аналитическим выражением 1-й производной функции у по ее аргументу х или проще — производной от у по х. Коротко производную обозначают:
В математике равенство (29) называют аналитическим выражением 1-й производной функции у по ее аргументу х или проще — производной от у по х. Коротко производную обозначают:
читают: игрек штрих по икс или проще — игрек штрих.
По предложению немецкого математика Г.Лейбница (1646-1716)
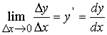 (30)
(30)
читают: дэ игрек по дэ икс, где d — первая буква слова дифференциал — differencial — разделитель.
Итак, аналитическое выражение производной (29) читается:
первой производной функции по своему аргументу называют отношение приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
2.2 Дифференцирование функции.
 Найдем производную функции у = 3х + 5. По (29) с учетом (28) будем иметь: т.е
Найдем производную функции у = 3х + 5. По (29) с учетом (28) будем иметь: т.е
для функции у = 3х + 5 ее производная y' = 3.
Сам процесс нахождения производной, т.е. определение приращения функции, деление его на приращение аргумента и нахождение предела полученного отношения называется математической операцией — дифференцированием.
По формуле (30) будем иметь:
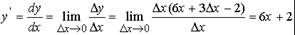 т.к.
т.к.
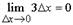 Т.е.
Т.е. 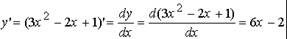
2.3 Основные правила дифференцирования.
1. (const)' = c' = 0.
Производная любого постоянного числа равна нулю.
Примеры: (5)' = 0; (–8)' = 0; (232)' = 0.
2. (х)' = 1.
Производная аргумента равна 1.
3. (c u)' = c u'.
Постоянное число можно выносить за знак производной.
Пример: (5 х)' = 5 x' = 5 1 = 5.
4. (u + v )' = u' + v'
Производная алгебраической суммы любого числа слагаемых равна этой же алгебраической сумме производных слагаемых.
Примеры: (3x – 8)' = (3x)' – (8)' = 3 1 -– 0 = 3; (kx + b)' = k.
5. Если 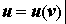 а ,
а , 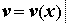 то
то 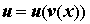 — сложная функция и [u(v(x))]’=u’v’.
— сложная функция и [u(v(x))]’=u’v’.
6. (un)' = n un–1 , где u — любая функция. Если u = x, то (xn)' = n x n–1.
Примеры: (х8)' = 8 x7; (x–3)' = –3 x–4;
((2x2 – 3x + 4)3)' = 3 (2x2 – 3x + 4)2 (4x – 3).
7. 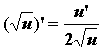 при u>0.
при u>0.
Примеры: 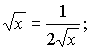
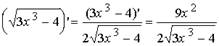
8. (sin u)' = u' cos u .
Если u = x, то (sin x)' = cos x .
Примеры: (3 sin x – 4x2)' = 3 cos x – 8x;
[sin(5x2 – 4)]' = (5x2 – 4)' cos (5x2 – 4) = 10 x cos(5x2 – 4).
9. (cos u)' = – u' sin u.
Если u = x, то (cos x)' = – sin x.
Примеры: (2 sin x – 4 cos x)' = (2 sin x)' – (4 cos x)' = 2 cos x + 4 sin x;
[cos (– x3 + 8)]' = – (– x3 + 8)' sin (– x3 + 8) = 3 x2 sin (– x3 + 8).
10. (u v)' = u' v + v' u .
Примеры: (3x2 sin x)' = (3x2)' sin x + 3x2 (sin x)' = 6x sin x + 3x2 cos x;
(sin 5x cos2x)' = (sin 5x)' cos2x + sin 5x (cos2х)' =
= 5 sin 5x cos2x – 2 cos x sin x sin 5x.
11. 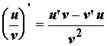
Примеры: 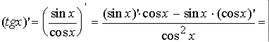
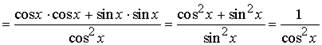 т.е
т.е
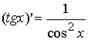
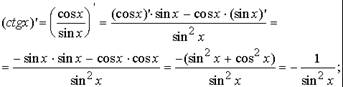
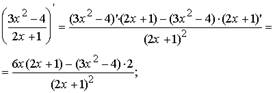
12. (ex)' = ex.
13. 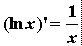
2.5 Геометрический смысл производной.
Пусть в точке М (x; f(x)) кривой y = f(x) существует касательная КТ к данной кривой (рис.25). Дадим аргументу х приращение х и отметим на кривой точку М1 (x + x; f(x + x)). Проведем секущую ММ1 и обозначим через 1 величину угла, образованного секущей с положительным направлением оси ОХ. Из треугольника ММ1А (прямоугольного) следует, что отношение 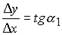 Если точка М1 будет перемещаться вдоль кривой, приближаясь к точке М, то x0. При этом секущая ММ1 и величина 1 меняются с изменением х. Предельным положением секущей при х0 будет прямая КТ — касательная к кривой в точке М, образующая с положительным направлением оси ОХ некоторый угол, его величину обозначим через.
Если точка М1 будет перемещаться вдоль кривой, приближаясь к точке М, то x0. При этом секущая ММ1 и величина 1 меняются с изменением х. Предельным положением секущей при х0 будет прямая КТ — касательная к кривой в точке М, образующая с положительным направлением оси ОХ некоторый угол, его величину обозначим через.
Так как  то
то 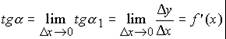 т.е. y' (M) = tg . (31)
т.е. y' (M) = tg . (31)
 Итак, с позиции геометрии производная функции у в заданной ее точке М есть тангенс угла наклона касательной, проведенной в точке М, с положительным направлением оси ОХ.
Итак, с позиции геометрии производная функции у в заданной ее точке М есть тангенс угла наклона касательной, проведенной в точке М, с положительным направлением оси ОХ.
Задача 4. Найти уравнение касательной к параболе y = 3x2 – 4x +5 в точке М1 с абсциссой х1 = 2.
Решение: Будем искать уравнение касательной в виде уравнения прямой с угловым коэффициентом, т.е. y = kx + b. Из уравнения (8) известно, что k есть тангенс угла наклона прямой к положительному направлению оси ОХ, т.е. k = y'(M1). Так как М1 принадлежит и касательной и параболе, то ее координаты удовлетворяют их уравнениям. Подставив х1 = 2 в уравнение параболы, найдем ординату у1 точки М1:
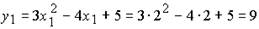 Значит М(2,9). Найдем y' = (3x2 – 4x + 5)' = 6x – 4. В точке М1
Значит М(2,9). Найдем y' = (3x2 – 4x + 5)' = 6x – 4. В точке М1
y'(x1) = 6x1 – 4 = 6 2 – 4 = 8. Значит k = 8. Подставив значение k = 8; х1 = 2; у1 = 9 в уравнение прямой, найдем b: 9 = 8 2 + b; b = – 7. Значит касательная к параболе y = 3x2 – 4x + 5 в точке М1(2,9) будет иметь уравнение y = 8x – 7.
2.6 Примеры непосредственного дифференцирования функций.
Пример 4. Найдите производную функции 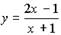 Вычислите y'(2).
Вычислите y'(2).
Решение: 1. 
Упражнения для самостоятельного решения.
2. Пользуясь определением производной, найдите производные следующих функций:
а) f(x) = 3x + 1 в точке х = 5;
б) (х) = 4х2 – 1, найдите (2);
в) h(x) = 5x2 +3x +8 в точке х = – 4;
г) g(t) = 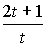 в точке t = 9;
в точке t = 9;
д) y(x) = ax2 + bx + c в точке х = 3;
е) f(x) = 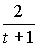 в точке t = 1;
в точке t = 1;
ж) h(x) = 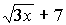 в точке х = 3;
в точке х = 3;
з) f(x) =  в точке х = 2.
в точке х = 2.
3. Найдите производную функции f(x) = 4x2 + 1 и докажите, что
4f'(x) – f(2) = 15.
4. Найдите производную функции f(x) = 5x2 + 6x и докажите, что f(2) + 2f'(–2) = 4.
2.7 Примеры дифференцирования по формулам.
Пример 1. Найдите производную функции f(x) = x2 + x – 7 . Вычислите f'(–1), f'(0), f'(3).
Решение: f'(x) = (x2 + x – 7)' = (x2)' + x' – 7' = 2x + 1 – 0 = –2x + 1
f'(-1) = 2 (-1) +1 = -1
f'(0) = 2 0 +1 = 1
f'(3) = 2 3 + 1 = 7
Пример 2. Найдите производную функции f(x) = x3 (x - 1).
Решение: f'(x) = (x3(x – 1))' = (x3)'(x – 1) + x3(x – 1)' =
= 3x2 (x – 1) + x3 (1 – 0) = 3x3 - 3x2 + x3 = 4x3 – 3x2.
Пример 3. Найдите производную функции а) 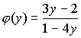
Решение: '(y) = 
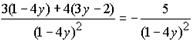
б) 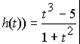
Решение: 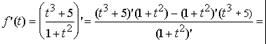
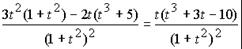
2.8 Производная сложной функции.
Производная сложной функции y = f((x)) находится по формуле y' = f'((x)) '(x) или y'x = y'u u'x, где u = (x).
Пример 1. Найдите производную функции y = (3x2 - 1)5.
Решение: Обозначим 3x2 - 1 = u, тогда y = u5.
Воспользуемся формулой y'x = y'u u'x.
Найдем: y'u = (u5)' = 5u4
u'x = (3x2 - 1)' = 6x, тогда
y'x = 5 (3x2 - 1)4 6x = 30x (3x2 - 1)4.
Пример 2. Найдите производную: y = (x2 +3x + 1)5.
Решение: y'x = ((x2 + 3x + 1)5)' = 5(x2 + 3x + 1)4 (2x + 3).
Пример 3. Найдите производную: 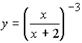
Решение: 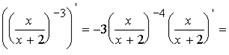
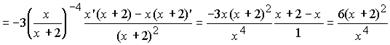
Пример 4. Найдите производную функции 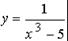
Решение: 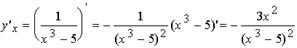
2.9 Дифференциал функции и дифференциал аргумента.
По определению производной 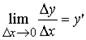 и по определению предела получим:
и по определению предела получим:  (32)
(32)
где — бесконечно малая величина (БМВ) при х 0. Умножая обе части (32) на х, получим: 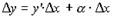 (33)
(33)
где х при х 0 тоже БМВ.
Лейбниц предложил обозначить
 (34)
(34)
и назвать это дифференциалом функции. Тогда, если у = х, то
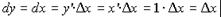 т.е.
т.е. 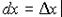 (35)
(35)
Откуда дифференциал аргумента — dx — равен приращению аргумента — х. Учитывая (35) и (33) можно (34) представить в виде:
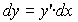 (36)или
(36)или 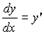 (36’)
(36’)
Пример. Найти дифференциал функции у=2х + sin x.
Решение: По формуле (36) получим: 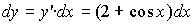
Отсюда формулами для нахождения дифференциала будут формулы для нахождения производной, где вместо знака производной перед функцией будет стоять символ d. Например:
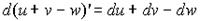 (37)
(37)
 (38)
(38)
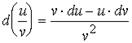 и т.д. (39)
и т.д. (39)
2.10 Геометрический смысл дифференциала функции.
Подставляя (36) в (33), получим:
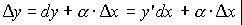 (37)
(37)
Так как  = БМВ, предел которой равен нулю при х 0, то
= БМВ, предел которой равен нулю при х 0, то
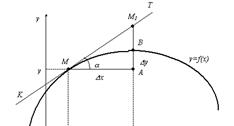
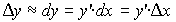 (38)
(38)
На рис. 27 рассмотрим геометрический смысл выражения (37).
Из прямоугольного ММ1А с учетом (36) и (37) получим: 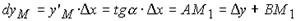 (39)
(39)
С учетом (37) и (39) можно сказать, что дифференциал функции в конкретной точке отличается от приращения функции в этой точке на бесконечно малую величину, соответствующую отрезку между точками пересечения вертикальной проекцией приращенного аргумента с графиком функции и с продолжением касательной, проведенной к графику в рассматриваемой точке.
Пример 1. Определить приближенное значение 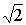
Решение: Рассмотрим функцию 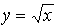 По формуле (38):
По формуле (38):
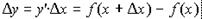 пусть х=2,25 х= – 0,25 , тогда
пусть х=2,25 х= – 0,25 , тогда
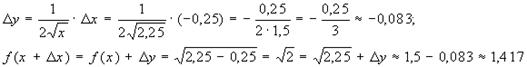
 Значит
Значит 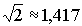
Пример 2. Найти абсолютную погрешность средней скорости спринтера в створе двух фотолучевых установок (ФЛУ), отстоящих друг от друга на расстоянии 5 м, если спринтер пробегает это расстояние за 0,422 с и ошибка в расстоянии за счет вертикальных колебаний тела составляет 20 см, а время определено с ошибкой 0,002с.
Решение: По условию примера мы имеем:  (м);
(м);
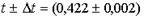 (c). Скорость
(c). Скорость 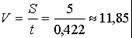 (м/с.).
(м/с.).
Дифференциал скорости согласно (41) будет:
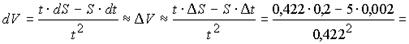
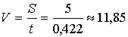
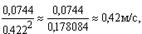 м/с, т.е.
м/с, т.е. 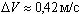 м/с и скорость имеют значение
м/с и скорость имеют значение  м/с.
м/с.
Для самостоятельного решения.
Найти дифференциалы и вторые производные следующих функций:
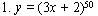
| 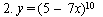
|
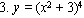
| 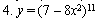
|
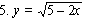
| 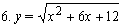
|
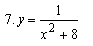
| 
|

| 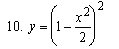
|
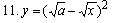
| 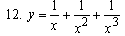
|
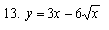
| 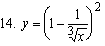
|
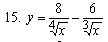
| 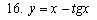
|
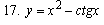
| 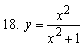
|
| 
|
| 
|
| Функция f(x) | Первая производная f'(x) | |
| 1. 1 | y = const | (C)'=0 |
| 2. | y = x | y` = 1 |
| 3. | y = xn | y' = nxn-1 |
| 4. | y = ax | y' = axln(a) |
| 5. | y = ex | y' = ex |
| 6. | y=kx +b | y`=k |
| 7. | y= 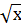
| 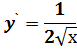
|
| 8. | 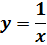
| 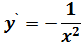
|
| 9. | y = loga(x) | y' = 
|
| 10. | y = ln(x) | y' = 1/x |
| 11. | y = sin(x) | y' = cos(x) |
| 12. | y = cos(x) | y' = -sin(x) |
| 13. | y = tg(x) | y' = 1/cos2(x) |
| 14. | y = ctg(x) | y' = -1/sin2(x) |
| 15. | y = arcsin(x) | у' = 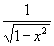
|
| 16. | y = arccos(x) | y' = - 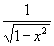
|
| 17. | y = arctg(x) | y' = 1/(1+x2) |
| 18. | y =arcctg(x) | y' = -1/(1+x2) |
Дифференциал.
Вычисление дифференциала.
Мы установили, что дифференциал функции У = f(x) имеет форму
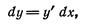
т. е. дифференциал функции 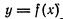 равен произведению производной этой функции на дифференциал ее аргумента.
равен произведению производной этой функции на дифференциал ее аргумента.
Пример 1. Найти дифференциал функции
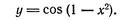
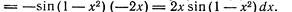 Решение По формуле (1) находим:
Решение По формуле (1) находим: 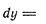
Пример 2. Найти дифференциал функции 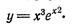
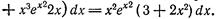 Решение. Находим:
Решение. Находим: 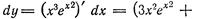
Дифференциалы высших порядков.
Из формулы 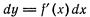 следует, что дифференциал функции
следует, что дифференциал функции 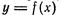 зависит от двух переменных, х и
зависит от двух переменных, х и 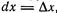 , причем dx от х не зависит.
, причем dx от х не зависит.
Рассмотрим дифференциал 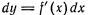 только как функцию от х, т. е. будем считать dx постоянным.
только как функцию от х, т. е. будем считать dx постоянным.
В этом случае можно найти дифференциал этой функции. Дифференциал от дифференциала функции 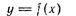 называется дифференциалом второго порядка, или вторым дифференциалом этой функции и обозначается
называется дифференциалом второго порядка, или вторым дифференциалом этой функции и обозначается 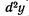 («де два игрек») или
(«де два игрек») или  («де два эф от икс»).
(«де два эф от икс»).
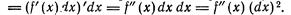 Таким образом,
Таким образом, 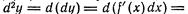
Принято скобки при степенях dx не писать, поэтому 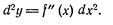
Аналогично определяются Дифференциалы третьего порядка: 
Вообще, дифференциалом n-го порядка называется дифференциал от дифференциала (n— 1)-го порядка:
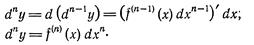
Таким образом, для нахождения дифференциала n-го порядка функции y = f(x) нужно найти производную n-го порядка от этой функции и полученный результат умножить на 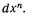 .
.
Пример. Найти дифференциалы первого, второго и третьего порядка функции
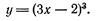
Решение. Находим соответствующие производные от данной функции:
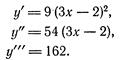
Следовательно,
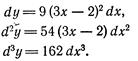
Приложение дифференциала приближенным вычислениям.
Рассмотрим функцию y = f(x), приращение которой

и дифференциал
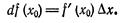
Выше было установлено, что при достаточно малых 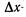 имеем
имеем
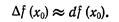
Так как вычислять df(xo) значительно проще, чем
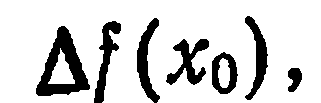 на практике формулу (3) применяют к различным приближенным вычислениям.
на практике формулу (3) применяют к различным приближенным вычислениям.
1. Вычисление приближенного значения приращения функции.
Пример 1. Найти приближенное значение приращения функции 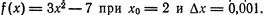
Решение. Применив формулу (3), получим:
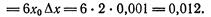
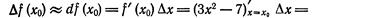 = 6х0Л* =.0,001
= 6х0Л* =.0,001
Посмотрим, какую погрешность мы допустили, вычислив дифференциал данной функции вместо ее приращения. Для этого найдем истинное значение приращения:
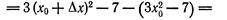
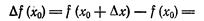
 |
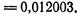
Далее, находим абсолютную погрешность приближения:
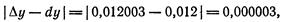
а затем и относительную погрешность:
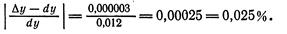
Погрешность приближения оказалась довольно малой, что еще раз подтверждает целесообразность применения формулы (3).
2. Вычисление приближенного числового значения функции. Из формулы (1) имеем
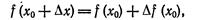
или
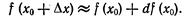
Пример 2. Найти приближенное значение функции 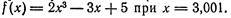
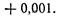 Решение. Представим х в виде суммы
Решение. Представим х в виде суммы 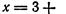
 Приняв хо = 3 и
Приняв хо = 3 и 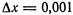 , найдем
, найдем 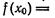
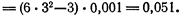

Следовательно,
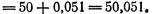

3.Приближенное вычисление степеней. Рассмотрим функцию 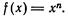 Применив формулу (4), получим
Применив формулу (4), получим

или
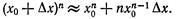
По этой формуле наводят приближенное значение степеней.
Пример 3. Найти приближенное значение степени
5,0133.
Решение. Представим данную степень в виде
(5 + 0,013)3. Приняв  по формуле
по формуле
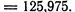 (5) найдем:
(5) найдем: 
1. Приближенное извлечение корней.
При 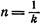 и
и 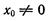 формула (5) примет вид
формула (5) примет вид
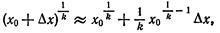
или
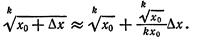
Формула (6), известная и по школьному курсу, дает возможность найти приближенные значения различных корней.
Пример 4. Найти приближенное значение корня 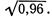
Решение. Представим данный корень в виде
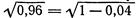
Приняв 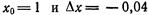 , по формуле (6) найдем:
, по формуле (6) найдем:
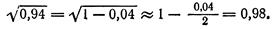
Закрепление материала:
1. Найти приближенные значения приращений следующих функций:

2. Сторона квадрата равна 5 см. Найти приближенное приращение его площади при увеличении его стороны на 0,01 см.
3. Шар радиуса R = 9 см был нагрет, вследствие чего его объем увеличился на  . На сколько (приближенно) удлинился его радиус?
. На сколько (приближенно) удлинился его радиус?
4. Найти приближенные значения следующих функций:
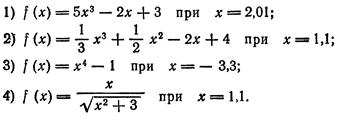
5. Найти приближенные значения степеней:
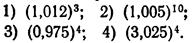
6. Найти приближенное значение корней:
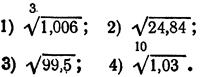
Неопределенный интеграл. Определенный интеграл, его свойства. Способы интегрирования.
Первообразная функция.
В дифференциальном исчислении мы решали задачу нахождения производной или дифференциала заданной функции. Однако, иногда, приходится находить по заданному дифференциалу функцию, от которой была взята производная, т.е. решать задачу, обратную дифференцированию.
Например, если известны путь S(t) мы можем найти v(t) , т.к. S¢(t) = v(t) , а теперь наоборот по скорости v(t) нужно найти S(t).
Первообразной называют функцию, восстанавливаемую по заданной ее производной или дифференциалу.
Итак, первообразной для заданной функции называется та функция, из которой заданная может быть получена дифференцированием.
Пример 1. Пусть 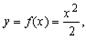 , тогда
, тогда 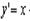 — производная для
— производная для 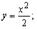
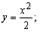 для функции
для функции  будет первообразной.
будет первообразной.
Пример 2. Пусть 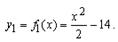 . Тогда
. Тогда  — производная для
— производная для 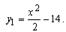 . Отсюда, для той же производной
. Отсюда, для той же производной  и функция
и функция 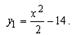 тоже будет первообразной (рис.30).
тоже будет первообразной (рис.30).
Свойство первообразных
Если какая-то функция 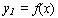 —первообразная для функции
—первообразная для функции 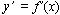 то и функция
то и функция  тоже первообразная для функции
тоже первообразная для функции 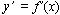 .
.
В математике принято явный вид первообразной записывать в общем виде так:
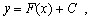
где 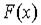 —часть функции у, содержащая аргумент х , т.е. изменяющаяся ее часть, а С — часть функции у, не содержащая аргумент х, т.е. не изменяющаяся ее часть — постоянная —
—часть функции у, содержащая аргумент х , т.е. изменяющаяся ее часть, а С — часть функции у, не содержащая аргумент х, т.е. не изменяющаяся ее часть — постоянная — 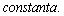
Пример.  можно записать в виде
можно записать в виде  ,где
,где 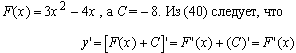
Определение. Дифференцируемая функция F(x), xÎ (a;b), называется первообразной функцией для f(x) на интервале (a;b), если выполняется равенство
F¢(x) = f(x)
Пример. f(x) =3x2
F1(x)=x3, F¢(x)=f(x)
F2(x) = x3+4, F¢(x)=(x3+4)¢ =3x2
F3(x) = x3-2, F¢=(x3-2)¢ =3x2
вообще F(x) = x3 + C является первообразной для f(x) =3x2, где С – константа.
Теорема. Если функция F(x) является первообразной для f(x), xÎ(a;b), то множество всех первообразных задается формулой F(x) + C, CÎR.
Совокупность всех первообразных функций f(x) на интервале (a;b) называется неопределенным интегралом от функции f(x) на (a;b) и обозначается символом: 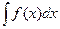 ,
,
где 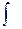 - знак интеграла,
- знак интеграла,
f(x) – подынтегральная функция
f(x)dx – подынтегральное выражение
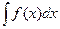 = F(x) + C
= F(x) + C
Нахождение функции по ее производной или по ее дифференциалу называется интегрированием функции. Правильность интегрирования проверяется дифференцированием.
Например. 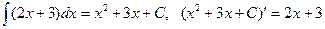
Cвойства интеграла
1. 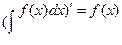
2. 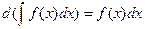
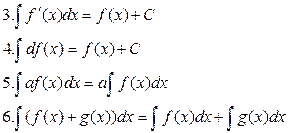
Таблица неопределенных интегралов
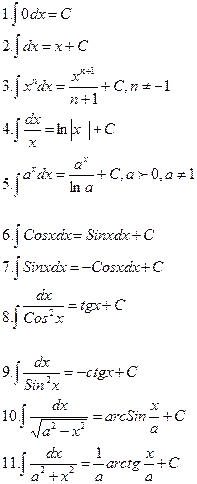
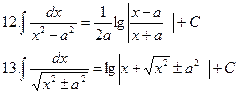
Способы интегрирования
I. Непосредственное интегрирование – применяется для интегрирования простых функций. Сводится к математическим преобразованиям приводящим интеграл к табличному виду.
Примеры:
1) 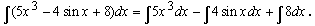
2) 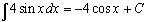 .
.
3) 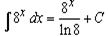 .
.
4) 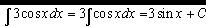 .
.
5) 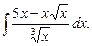
Решение. Воспользоваться определением степени с дробным показателем 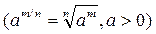 , правилами действий над степенями с одинаковыми основаниями (am an = a m + n , am/an = a m – n ), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеем
, правилами действий над степенями с одинаковыми основаниями (am an = a m + n , am/an = a m – n ), правилом деления суммы на число и найдем интеграл от каждого слагаемого отдельно. Имеем 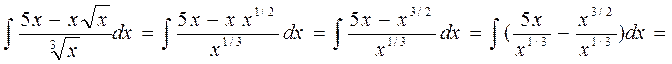
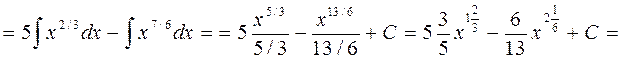
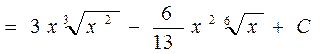
II. Интегрирование методом подстановки (введение новой переменной). Применяется для интегрирования сложных функций. Сводится к выполнению следующих шагов алгоритма:
Алгоритм
1. Ввести новую переменную
2. Найти дифференциал переменной равный произведению производной функции на дифференциал аргумента.
3. Вычислить дифференциал аргумента.
4. Подставить введенные величины под знак интеграла.
5. Методом математических преобразований привести интеграл к табличному интегралу и найти его значение.
6. Вернуться к первоначальной переменной.
Примеры:
 1)
1) 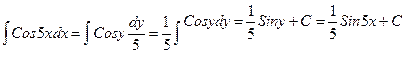
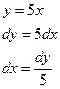
2) 
Решение. Произведем подстановку 5 – 3x = t, тогда –3 dx = dt, откуда  Далее получаем
Далее получаем

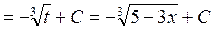
3) 
Решение. Сначала положим 2 + cosx = t, тогда –sin x dx = dt, откудаsinx dx = - dt. Далее получаем 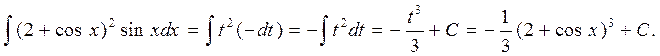 III. Интегрирование по частям
III. Интегрирование по частям
(uv)¢ =u¢v +v¢u
d(uv) = vdu + udv
udv =d(uv) – vdu
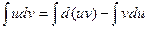
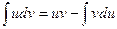 - формула интегрирования по частям
- формула интегрирования по частям
Примеры:
1) 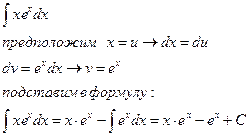
2)

Вычислить:
1. 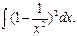
Решение: 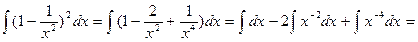
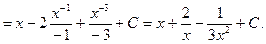
2. 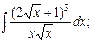
3. 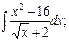
Определенный интеграл.
Теорема 1. Если функция f(x) монотонна на отрезке [a;b], то она интегрируема на этом отрезке.
Теорема 2. Если функция f(x) непрерывна на отрезке [a;b], то она интегрируема на этом отрезке
Если функция f(x) интегрируема на отрезке[a;b], то выражение
 - называется определенным интегралом. Величины a,b называются пределами интегрирования, соответственно а – верхний предел, b – нижний предел.
- называется определенным интегралом. Величины a,b называются пределами интегрирования, соответственно а – верхний предел, b – нижний предел.
Свойства определенных интегралов
1. Для любого действительного числа a
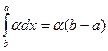 (1)
(1)
2. Если f(x) интегрируема на отрезке [a;b], то для любого действительного числа a функция f(x0 также интегрируема на [a;b].
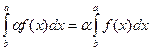 (2)
(2)
3. Если f(x) и g(x) интегрируемы на отрезке [a;b], то и сумма f(x) + g(x) также интегрируема на [a;b].
 (3)
(3)
4. Если на отрезке [a;b] функция f(x) и g(x) интегрируемы и f(x) £g(x), то
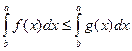 (4)
(4)
5. Если функция f(x) интегрируема на отрезке [a;b], то она интегрируема на любом отрезке, содержащемся в [a;b].
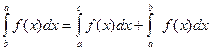 (5)
(5)
6. Если a=b, то 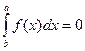 (6)
(6)
7. Если a < b , то  (7)
(7)
Теорема. Если функция f(x) непрерывна на отрезке [a;b], а функция F(x) является первообразной для функции f(x) на [a;b], то справедлива формула
| |
| |
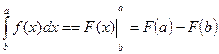 - формула Ньютона-Лейбница.
- формула Ньютона-Лейбница.
Способы интегрирования
I. Непосредственное интегрирование – применяется для интегрирования простых функций. Сводится к математическим преобразованиям приводящим интеграл к табличному виду и дальнейшему его вычислению с помощью формулы Ньютона-Лейбница.
1) 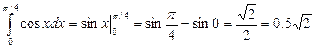
2) 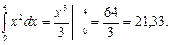
3) 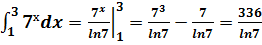
1. Интегрирование методом подстановки (введение новой переменной). Применяется для интегрирования сложных функций. Сводится к выполнению следующих шагов алгоритма:
Алгоритм
1. Ввести новую переменную
2. Найти дифференциал переменной равный произведению производной функции на дифференциал аргумента.
3. Вычислить дифференциал аргумента.
4. Изменить границы интегрирования.
5. Подставить введенные величины под знак интеграла.
6. Методом математических преобразований привести интеграл к табличному интегралу и найти значение первообразной.
7. Используя формулу Ньютона-Лейбница найти числовое значение интеграла.
1) 
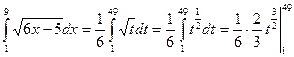 =
= 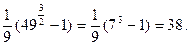
Сделаем подстановку: 6∙x – 5 = t; 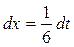
Вычислим новые пределы: при xн = 1, tн = 1; xв = 9, tв = 49.
2) : 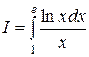 .
.
Сделаем замену: ln x = t или x = et, тогда если x = 1, то t = 0, а если x = e, то t = 1. В результате получим: 
5.12. Геометрический смысл определенного интеграла.
С позиции геометрии определенный интеграл численно равен площади фигуры ограниченной: сверху (или снизу) — участком графика под-интегральной функции от x = a до x = b; справа и слева — вертикалями x = a и x = b; снизу (или сверху) — отрезком b – a оси ОХ.
Это свойство определенного интеграла дает возможность через него аналитически определять площади плоских фигур и наоборот, по площадям фигур графически (приблизительно) находить значение определенного интеграла.
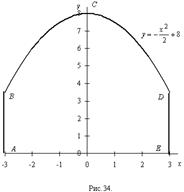 Задача 1. Определить площадь фигуры (SABCDE), изображенной на рисунке 34.
Задача 1. Определить площадь фигуры (SABCDE), изображенной на рисунке 34.
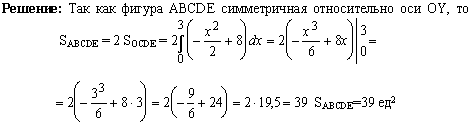
Закрепление материала.
1. 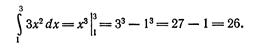
2. 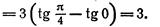
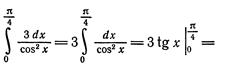
3. 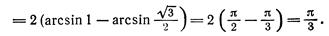

4. 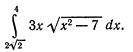
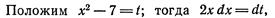
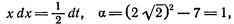
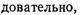
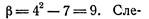
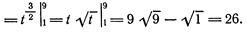
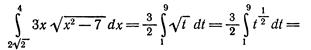
5. 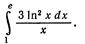
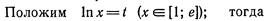
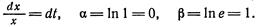
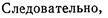
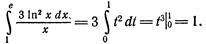
Решение прикладных задач с помощью определенного интеграла.
Определение площади криволинейной трапеции.
Фигура ограниченная графиком функции у=f(х), прямыми х=а, х=в и отрезком 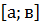 оси ОХ называется криволинейной трапецией.
оси ОХ называется криволинейной трапецией.
Рассмотрим различное расположение фигуры в осях координат:
1. Фигура расположена над осью ОХ. Площадь фигуры ограниченной линиями у=f(х), прямыми х=а, х=в и отрезком 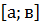 оси ОХ вычисляется по формуле:
оси ОХ вычисляется по формуле:
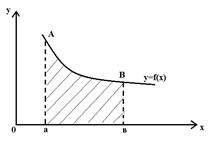
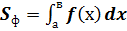
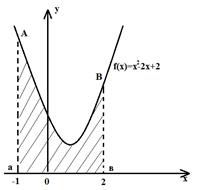
Пример: Вычислить площадь плоской фигуры ограниченной линиями у=х2-2х+2, х=1,х=2 и осью ОХ.
1. у=х2-2х+2- парабола, ветви  , вершина:
, вершина: 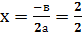 =1, у=12-2∙1+2=1; (1;1)
=1, у=12-2∙1+2=1; (1;1)
| х | 2. | 3. | 4. | |
| у | 5. |
2. Х=1- прямая ║ оси ОХ  (1; 0)
(1; 0)
3. Х=2- прямая ║ оси ОХ 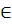 (2; 0)
(2; 0)
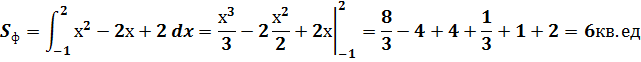
1.  Фигура расположена под осью ОХ. Пусть функция у=f(х),
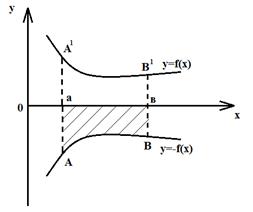
Фигура расположена под осью ОХ. Пусть функция у=f(х), 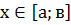 неположительная непрерывная функция. В этом случае график расположен под осью ОХ. Рассмотрев вспомогательную функцию у= - f(х) получим площадь фигуры аА1В1в, ограниченной графиком функции у= - f(х) . Так как фигуры равны, то равны и их площади.
неположительная непрерывная функция. В этом случае график расположен под осью ОХ. Рассмотрев вспомогательную функцию у= - f(х) получим площадь фигуры аА1В1в, ограниченной графиком функции у= - f(х) . Так как фигуры равны, то равны и их площади.

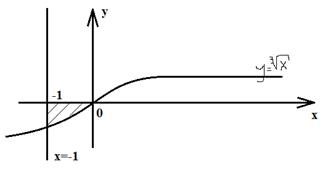
Пример: Вычислить площадь фигуры ограниченной линиями 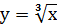 , х= - 1 и осью ОХ.
, х= - 1 и осью ОХ.
1. 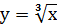 - кубическая парабола, 1 и 3 четверть
- кубическая парабола, 1 и 3 четверть
| х | |||
| у |
2. х= -1- прямая ║ оси ОХ  (-1; 0)
(-1; 0)
3. у=0 – ось ОХ

 3. Фигура не является криволинейной трапецией. Рассмотрим фигуру ограниченную отрезками прямых х=а, х=в и графиками функций у=f(x) и у=g(x). Эту фигуру можно рассматривать как разность криволинейных трапеций аАВв и аМNв, поэтому формула для вычисления площади
3. Фигура не является криволинейной трапецией. Рассмотрим фигуру ограниченную отрезками прямых х=а, х=в и графиками функций у=f(x) и у=g(x). Эту фигуру можно рассматривать как разность криволинейных трапеций аАВв и аМNв, поэтому формула для вычисления площади
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|