Хелпикс

Главная

Контакты

Случайная статья



xj= xmin + ( j-1)*D; xj+0.5= (xj + xj+1)/2.

⇐ ПредыдущаяСтр 2 из 2


Задание 3

3.1. Построим гистограмму выборки ХВ как удобную форму представления выборочного распределения. Для этого разобьем наблюдаемый интервал значений в выборке на m равновеликих интервалов

xmin= 1; xmax= 12; m=5; D= 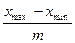 =2,2

Количество интервалов разбиения mвыбирается исходя из свойств выборки, рекомендуется использовать формулу m=1+3,2*lg(n), m=5,73 примем m=5. Граничные точки интервалов hj=[xj , xj+1], j=1,.., mи их центры xj+0.5 вычисляем по формулам следующим образом:

xj= xmin + ( j-1)*D;   xj+0.5= (xj + xj+1)/2.

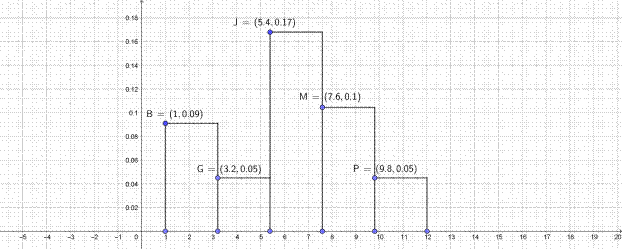
Подсчитав для каждого интервала частоты попадания в него элементов выборки nj и относительные частоты wj =nj/n , сведем все результаты расчета наблюдаемых частот nj, wjв следующую таблицу 3 и построим гистограмму относительных частот (рис. 3). Высота прямоугольников (относительных частот) очевидно равна  wj /D .                                                                   Таблица 3

hj

1 - 3,2

3,2 - 5,4

5,4 - 7,6

7,6 - 9,8

9,8 - 12

å

xj+0.5

2,1

4,3

6,5

8,7

10,9

nj

wj

0,2

0,1

0,37

0,23

0,1

wj /D

0,091

0,045

0,168

0,1045

0,045

 


Рис.3. Гистограмма относительных частот

 

Литература

 

1. Гмурман В.Е. Теория вероятностей и математическая статистика. М., “Высшая школа”, 2001.

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., “Высшая школа”, 2001.

 


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.