Контакты

Случайная статья

Произведение нулевого вектора на любое число есть нулевой вектор.

⇐ ПредыдущаяСтр 2 из 2

Произведение нулевого вектора на любое число есть нулевой вектор.

Векторы a→ и ka→ коллинеарны для любого k. Если два вектора a→ и b→ коллинеарны, то существует такое число k, что a→ =kb→.
Произведение любого вектора на число нуль есть нулевой вектор.
Для любых векторов a→ и b→ и чисел k и l справедливы следующие законы:

сочетательный: (kl)a→=k(la→);

первый распределительный: k(a→+b→)=ka→+kb→;

второй распределительный: (k+l)a→=ka→+la→.

Практическая работа

Внимание! 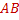→ в конспекте вектор располагайте над АВ.

1. Упрости выражение 4n→−3(2m→−3p→)+4(3n→+2m→+2p→) и выбери правильный вариант ответа:

а) 17n→+2m→+17p→

б) 17n→+m→+16p→

в) 17n→+m→+17p→

г) 16n→+2m→+17p→

2. Дан параллелепипед ABCDA1B1C1D1.

Указание: начертите параллелепипед ABCDA1B1C1D1.

Который из данных векторов равен сумме векторов B1C1−→−− и AB−→−?

а) DC1→−−

б) A1C1→−−

в) DB→−

с) A1B→−

3.

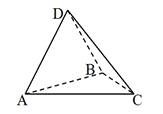
ABCD — тетраэдр.

Определи, какой вектор является суммой векторов CD→ и DA→ —

Назови вектор, который является разностью векторов CA→ и BA→ —

4.

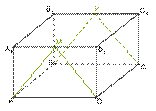
Дан параллелепипед ABCDA1B1C1D1. Точки M и K — середины рёбер A1D1 и B1C1 соответственно.

Найди (вводи с латинской раскладки):

а). KC−→− + BK→ =

б). AB→ − AD→ =

5. Дан параллелограмм ABCD. Точки E,F,G,H являются соответственно серединами сторон AB,BC,CD,AD. O — произвольная точка пространства.

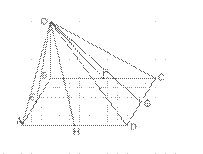
Вырази вектор DO→+OH→ через вектор BC→:

а) 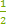BC→

б) −2BC→

в) − 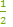BC→

с) 2BC→

Контрольные вопросы:

1. Дайте определение противоположных векторов.

2. Запишите правило треугольника для сложения векторов.

3. Запишите правило параллелограмма для сложения векторов.

4. Запишите правило умножение вектора на число.

5. . Запишите правило сложения векторов, когда их больше двух

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.