Показатели вариации

2. Показатели вариации

2.1 Вариационный размах

Вариационный размах (амплитуда колебаний) – это самый простой показатель вариации.

Вариационный размах признака рассчитывается как разность между максимальной и минимальной вариантами определённого количества признака в статистической совокупности.

Вариационный размах рассчитывают следующим образом:

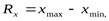
где:

R_х – размах вариации признака;

- соответственно конечная (максимальная) и начальная (минимальная) варианты.

Основной недостаток вариационного размаха заключается в том, что он не отражает внутренних изменений признака и полностью зависит от отдельных случаев, оказывающихся на обоих полюсах ранжированного ряда. Поэтому вариационный размах используется для поверхностной характеристики вариации признака в статистической совокупности.

2.2. Среднее квадратическое отклонение

Среднее квадратической отклонение рассчитывается по простой и взвешенной формах.

Для ранжированного ряда рассчитывают невзвешенное (простое) среднее квадратической отклонение по следующей формуле:

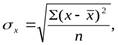
Где

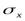- среднее квадратической отклонение вариационного признака;

х – индивидуальные варианты в ранжированном ряду;

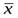- среднее значение признака в статистической совокупности;

n – число вариант в ряду.

Взвешенное среднее квадратическое отклонение рассчитывают для дискретного ряда по формуле:

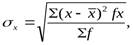
где f_х – частота (веса) в вариационном ряду.

Расчет среднего взвешенного квадратического отклонения осуществляют в определенной последовательности:

1. По данным дискретного или интервального вариационного ряда находят среднее арифметическое взвешенное значение признака – ( ).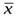

2. Рассчитывают индивидуальные линейные отклонения по каждой варианте –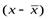

3. Полученные линейные отклонения вариант возводят в квадрат -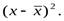

4. Квадраты линейных отклонений взвешивают - 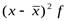и суммируют - .

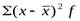5. Находят сумму накопленных частот (весов) - (Σ f).

6. Сумму взвешенных квадратов делят на сумму накопленных частот (весов) - 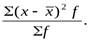полученный результат представляет собой средний квадрат отклонений (дисперсию). Дисперсия как показатель колеблемости признака не играет какой-либо самостоятельной роли при оценке вариации признака в статистической совокупности. Вместе с тем дисперсия представляет собой особый интерес при рассмотрении и применении дисперсионного метода.

7. Из среднего квадрата отклонений (дисперсии) извлекают квадратный корень, в

результате чего получаем среднее квадратическое отклонение.

Целесообразно обратить внимание на то, что среднее квадратическое отклонение измеряется в тех же единицах, что и варианты изучаемого признака в статистической совокупности. Оно характеризует среднюю колеблемость вариант в этой совокупности и широко используется в качестве одного из более точных и объективных показателей вариации не только в статистике, но и в технике, биологии, других отраслях знаний.

⇐ Предыдущая 123 Следующая ⇒