СОБЫТИЕ, ВЕРОЯТНОСТЬ СОБЫТИЯ СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ

СОБЫТИЕ, ВЕРОЯТНОСТЬ СОБЫТИЯ СЛОЖЕНИЕ И УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ

Вероятностьюсобытия A называется отношение числа исходов m, благоприятствующих наступлению данного события 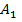к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е. –вероятность случайного события Вероятность любого события не может быть меньше нуля и больше единицы, т.е. 0≤P(A)≤1

Невозможному событию соответствует вероятность P(A)=0, а достоверному – вероятность P(A)=1

теорема сложения вероятностей несовместных событий.

Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

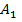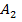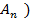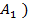P(A+B)=P(A)+P(B); P( + +…+ =P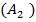( +P +…+P( ).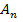

Теорема сложения вероятностей совместных событий.

Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

P(A+B)=P(A)+P(B)-P(AB)

Для трех совместных событий имеет место формула:

P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)

Событие, противоположное событию A (т.е. ненаступление события A), обозначают 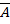. Сумма вероятностей двух противоположных событий равна единице: P(A)+P( 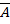)=1

Вероятность наступления события A, вычисленная в предположении, что событие B уже произошло, называется условной вероятностью события A при условии B и обозначается 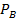(A) или P(A/B).

Если A и B – независимые события, то

P(B)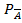- (B)= (B).

События A,B,C,… называются независимыми в совокупности, если вероятность каждого из них не меняется в связи с наступлением или ненаступлением других событий по отдельности или в любой их комбинации.

12 3 Следующая ⇒