Программа Истоминой. Программа Аргинской. Программа Петерсона

Программа Истоминой

М4И ч 2 стр 30

По программе Истоминой отдельного определения «умножение на целое число» не вводится. Дети должны самостоятельно вывести правило, а затем сравнить его с рассуждением в учебнике.

Программа Аргинской

М4А Ч1 СТР 67-68

Аргинская подводит к правилу через создание проблемной ситуации, так как одно число при умножении заканчивается нулем. Вместе с этим она приводит 2 ситуации: в одной нуль мешает при умножении и с ним умножать неудобно, а во второй нуль просто перенесли и он не мешает вычислением.

Программа Петерсона

М3П Ч1 СТР40

Петерсон сразу же после повторения сочетательного свойства умножение переходит к определению умножение круглого числа. Петерсон просто дает примеры вычисления в столбик чисел, оканчивающихся нулями, без подробных разъяснений и записей.

На этом этапе рассматриваем частные случаи, главным из которых является случай с 00 в первом множителе а) в середине, б) на конце первого множителя. Сначала разбираем устный случай, например,

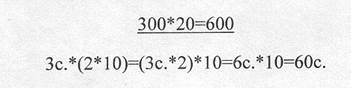
Выполняем несколько подобных вычислений и делаем вывод, что можно умножать, не обращая внимание на 0 на конце множителей, а затем на конце произведения приписать столько 0, сколько их было на конце первого и второго множителей вместе. Опираясь на этот вывод, выполняем письменные вычисления, например,

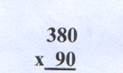
Т.е. нули оставляем в стороне, а затем приписываем их на конце произведения. Выполнив несколько подобных вычислений, обобщаем вывод и для приёма умножения столбиком.

(Моро 4 класс 2 часть стр.15)

⇐ Предыдущая 1 23