III. Эксперимент (моделирование)

1 класс

Когда изучают прием [ ]+3, чтобы доказать истинность предположения, что 5+3=8, можно вычислить этот результат тремя способами: 5+2+1=8; 5+1+2=8 и 5+1+1+1=8

2 класс

Например, чтобы доказать истинность предположения: Чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.

Т.е. (2+7)+3=2+(7+3)

Необходимо выполнить вычисления.

(2+7) + 3 = 10+3 = 12

2+(7+3) = 12

3 класс

Чтобы доказать истинность предположения, что разделить сумму на число можно двумя способами: (6+4):2=10:2 и (6+4):2=6:2+4:2, вычисляем значение этих выражений. Приходим к выводу, что ответ одинаковый. Следовательно, предположение верно.

(6+4):2=10:2=5

(6+4):2=6:2+4:2=3+2=5

4 класс

Чтобы доказать истинность предположения, что умножить число на сумму можно тремя способами: 6*(3*4)=6*12; 6*(3*4)=(6*3)*4; 6*(3*4)=(6*4)*3, вычисляем значение всех трех выражений. Приходим к выводу, что ответ одинаковый. Следовательно, предположение верно.

6*(3*4)=6*12=72

6*(3*4)=(6*3)*4=18*4=72

6*(3*4)=(6*4)*3=24*3=72

III. Эксперимент (моделирование)

1 класс

При изучении количественного счета, предполагаем, что результат не зависит от размера предметов, от плотности ряда. Доказательство модель:

- Чем отличаются ряды? (круги разного размера, по-разному расположены)

Предлагаем посчитать количество кругов в каждом ряду, в каждом ряду 4 круга. Следовательно, предположение верно.

2 класс

Когда таблица деления еще не изучена, при решении задач используют модели. Например, доказать, что 6:2=3 можно по модели:

6 квадратов разделили на ряды, в каждом ряду по 2 квадрата. Посчитайте по рисунку, сколько получилось рядов? (3 ряда)

3 класс

Чтобы доказать, что в 1 квадрантом дм 100 квадратных см, используем модель:

Это модель одного квадратного дм, он разбит на квадратные см, дети по модели пересчитывают количество квадратных см в одном квадратном дм.

4 класс

Чтобы доказать, что часть прямоугольника больше, чем часть этого прямоугольника используем модель:

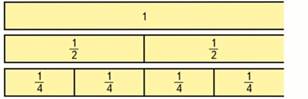
IV. Дедуктивные умозаключения – основной способ доказательства истинности в математике. Суть сводится к тому, что на основе общего суждения, о предмете данного класса и некоторого единичного суждения о каком-то предмете, высказывается новое единичное суждение о том же предмете.

Общее суждение– общая посылка;

Одно единичное суждение– это частная посылка;

Новое единичное суждение– умозаключение.

1 класс

Для сознательного выполнения дедуктивных умозаключений необходима большая подготовительная работа, направленная на усвоение вывода, закономерности свойства в общем виде, связанная с развитием математической речи.

Например, проводится длительная работа с принципами построения натурального ряда, это позволяет подвести учащихся к тому, что: «Прибавляя к числу единицу, мы получаем следующее число, а отнимая единицу - предыдущее число». Детям в течение ряда уроков предлагают выполнять действия с предметами, их пересчитыванием и, наконец, в результате длительной целенаправленной работы их подводят к выводу, который становится общей посылкой в проведении дедуктивных рассуждений при составлении таблиц сложения и вычитания единицы. Поэтому, приступая к составлению таблиц, необходимо прежде всего сосредоточить внимание учащихся на общем выводе и показать образец рассуждений:

1. если к числу прибавим 1, получим следующее число;

2. к одному прибавим 1, получим следующее число 2;

3. к двум прибавим 1, получим следующее число 3 и т.д.

· Примером одного из первых дедуктивных рассуждений в начальном обучении математике является рассуждение «2<3, потому что 2 при счете называют раньше, чем 3». С его помощью из одного общего суждения (общей посылки): если одно число при счете называется раньше другого, то это число будет меньше; и одного частного суждения (частной посылки): 2 при счете называют раньше 3, выводится новое частное суждение (заключение): 2<3. Получению вывода: «Чтобы узнать, на сколько единиц одно число больше (меньше) другого, нужно из большего числа вычесть меньшее» – должна предшествовать большая работа с предметной наглядностью, т.е. с рассмотрение конкретных частных случаев.

· При решении простых задач на разностное сравнение имеет смысл уже обращаться к дедуктивным рассуждениям, используя наглядность только на этапе решения задачи. Учащиеся рассуждают так: «Чтобы узнать, на сколько одно число больше другого, нужно из большего числа вычесть меньшее (общая посылка). У Димы было 6 марок, у Миши 2 марки. На сколько марок больше у Димы, чем у Миши (частная посылка). Умозаключение: значит, нужно из марок Димы вычесть марки Миши».

2 класс

· Общая посылка: "Умножением называют сложение одинаковых слагаемых". При выполнении упражнений на замену суммы одинаковых слагаемых умножением и наоборот, учащиеся рассуждают так:

Частная посылка: 7+7+7 (число 7 взяли слагаемым 3 раза).

Умозаключение: 7 умножили на 3.

· Иногда возможно использование нескольких способов доказательства суждения. При изучении темы «Единицы площади» учащимся предлагается задание:

Во сколько раз площадь прямоугольника АВСD больше прямоугольника КМЕО? Запиши ответ числовым равенством.

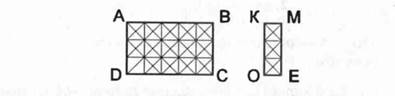
Маша записала такие равенства: 15:3=5, 30:6=5

Миша - такое равенство: 60:12=5

Кто из них прав? Как они рассуждали?

Для обоснования суждений, высказанных Машей и Мишей, учащиеся могут использовать способ дедуктивных рассуждений. Общая посылка - правило кратного сравнения чисел. (Чтобы узнать во сколько раз одно число больше или меньше другого, нужно большее число разделить на меньшее.)

В этом случае можно использовать и практический метод доказательства, в этом случае дети опираются на приведённый рисунок. (Источник: учебное пособие «Методика преподавания математики Н.Б.Истомина)

· Правильно ли решено выражение: 45+3=(40+5)+3=40+8=48?

Ученик рассуждает: "Чтобы к сумме чисел прибавить число, можно это число прибавить к одному слагаемому и к полученному результату прибавить другое слагаемое. (Общая посылка) Число 3 прибавили к второму слагаемому 5, получили 8 и потом прибавили второе слагаемое 40 и получили 48. (Частная посылка) Пример решен верно.(Умозаключение)

В рассмотренных примерах общее суждение использовалось в явном виде. В некоторых случаях они могут быть использованы и в неявном, скрытом виде. Например, решая тот же пример 45+3 ученик может рассуждать так: "45 это сумма чисел 40 и 5. К 5 прибавили 3, получили 8 и к 8 прибавим 40, получим 48". В таких случаях учителю полезно время от времени, для проверки понимания, спросить общее правило, которое и является общим суждением.

3 класс

· Является ли число 28 четным?

Общее суждение: Если число делится на 2, то оно четное.

Частное суждение: Число 28 делится на 2.

Умозаключение: Число 28 является четным.

· При решении задачи: «В одной книге 48 страниц, а в другой 16 страниц. Во сколько раз больше страниц в первой книге, чем во второй?» рассуждение строится таким образом:

Общая посылка: задачи, в которых требуется узнать во сколько раз одно число больше или меньше другого, решаются делением.

Частная посылка: в этой задаче надо узнать, во сколько раз 48 больше 16. Заключение: для ответа на вопрос задачи надо 48 разделить на 16».

· При решении выражений на порядок действий, рассуждения учащихся носят дедуктивный характер. В качестве общей посылки выступает правило выполнения порядка действий в выражении, в качестве частной посылки – конкретное числовое выражение, при нахождении значения которого учащиеся руководствуются правилом порядка действий.

4 класс

По учебнику Н.Б.Истоминой (и по некоторым другим программам) дети знакомятся с уравнением только в 4 классе.

Например, требуется решить уравнение 7*х=14

Для нахождения неизвестного множителя используется правило: «Если значение произведения разделить на один множитель (известный), то получим другой (значение неизвестного множителя).

Это правило - общая посылка.

В данном уравнении произведение равно 14, известный множитель - 7. Это частная посылка. Умозаключение: Нужно 14 разделить на 7, получим 2.

⇐ Предыдущая 12