Доказательство

Доказательство

Так как в результате n независимых испытаний, проведенных в одинаковых условиях, событие A наступает с вероятностью 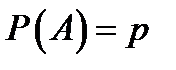, следовательно, противоположное ему событие с вероятностью .

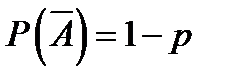Обозначим A_i — наступление события A в испытании с номером i. Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате n опытов событие A наступает k раз, тогда остальные n − k − раз это событие не наступает. Событие A может появиться k раз в n испытаниях в различных комбинациях, число которых равно количеству сочетаний из nэлементов по k. Это количество сочетаний находится по формуле:

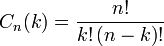При этом вероятность каждой комбинации равна произведению вероятностей:

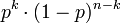Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли:

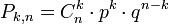где q = 1- p

Рассмотрим примеры применения:

Пример 1. Вероятность выхода за границы поля допуска при обработке деталей на токарном станке равна 0,07. Определить вероятность того, что из пяти наудачу отобранных в течение смены деталей у одной размеры диаметра не соответствуют заданному допуску.

Решение. Условие задачи удовлетворяет требования схемы Бернулли. Поэтому, полагая 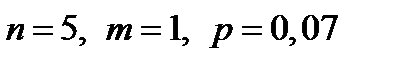, по формуле получаем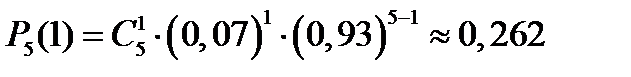

Ответ: 0,262

Пример 2. Наблюдениями установлено, что в некоторой местности в сентябре бывает 12 дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце 8 дней 3 дня окажутся дождливыми?

Решение.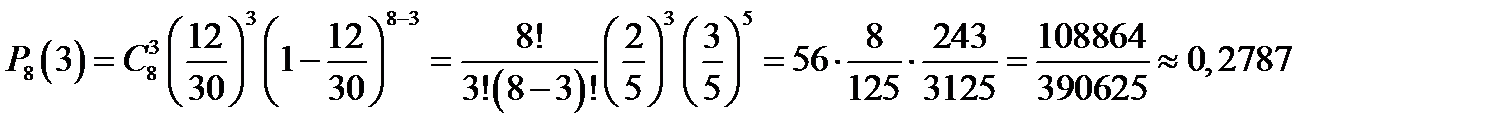

Ответ: 0,2787

Пример 3.Вероятность приема радиосигнала при каждой передаче равна 0,8. Найти вероятность того, что при пятикратной передаче сигнал будет принят ровно 4 раза. Ответ. 0,41.

Пример 4.Монета подбрасывается 10 раз. Найти вероятность того, что «герб» выпадает ровно 8 раз. Ответ. 0,044.

VI. Применение знаний при решении типовых примеров и задач.

Решить задачи типа:

1. Баскетболист забрасывает мяч в корзину с вероятностью попадания Р=0,4. Что вероятнее: ожидать попадание трех мячей при четырех бросках или попадание четырех мячей при шести бросках?

2. Всхожесть семян данного сорта растений оценивается вероятностью 0,8. Найти вероятность, что из пяти посеянных семян взойдет не меньше четырех. Ответ. 0,74.

3. Сколько испытаний потребуется для того, чтобы сделать вероятность события, которое произошло хотя бы один раз, равной не менее 0,5, если вероятность этого события при одном испытании равна 0,01?

Ответ. Не менее 70 испытаний.

4. При стрельбе в тире вероятность попадания пули в мишень равна 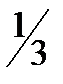. Сколько раз нужно выстрелить, чтобы вероятность по меньшей мере одного попадания в мишень была больше чем 0,9?

Ответ. Более 6 раз.

Самостоятельное применение знаний, умений и навыков.

Провести самостоятельную работу с выборочной проверкой.

Примерное содержание работы:

1. Вероятность того, что расход электроэнергии на протяжении одних суток не превысит установленной нормы, равна 0,75. Найти вероятность того, что в ближайшие шесть суток расход электроэнергии в течение четырех суток не превысит норму.

2. В цехе имеется шесть моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 мотора; б) включены все моторы, в) выключены все моторы. Ответ. а) 0,246; б) 0,262; в) 0,000064.

Подведение итогов занятия.

Домашнее задание.

Стр. 355-358 п14.3, сделать конспект, № 14.13 (по желанию).

⇐ Предыдущая 1 23