
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Изучение нового материала. Домашнее задание. Ход урока. Организационный момент.
3. Изучение нового материала
4. Домашнее задание
Ход урока
1.Организационный момент.
2.Повторение опорных знаний учащихся. Повторить с учащимися определение, формулы, свойства сочетаний.
Решить задачи 1—3 устно, 4—8 письменно;
1.Вероятность того, что день будет дождливым, равна 0,7. Найти вероятность того, что день не будет дождливым.
Решение: Ответ. 0,3.
2. В урне 10 белых и 15 черных шаров. Из урны наудачу вынимают один шар. Найти вероятность того, что этот шар белый. Ответ. 0,4. ,
3. В урне 10 белых и 15 черных шаров. Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми. Ответ. 0,15.
4. В первом ящике содержится 20 деталей, из них 15 стандартных, во втором — 30 деталей, из них 6 стандартных. Найти вероятность того, что наудачу извлеченная деталь из наудачу взятого ящика стандартна. Ответ. 0,475.
5. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса. Ответ. 0,496.
6. Три электрические лампочки последовательно включены в цепь. Вероятность того, что одна (любая) лампочка перегорит, если напряжение в сети превысит номинальное, равна 0,6. Найти вероятность того, что при повышенном напряжении тока в цепи не будет. Ответ. 0,936.
7. В группе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Найти вероятность того (если считать выбор случайным), что выбраны: а) два мальчика; б) две девочки; в)девочка и мальчик.
Ответ, а) 0,152; б) 0,352; в) 0,497.
8. Имеется три урны с шарами: в I урне - 4 белых и 5 черных шаров, во II - 5 белых и 4 черных шара, в III - 6 белых шаров. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар окажется белым.
Ответ. 0,667.
3.Изучение нового материала.
Прежде чем рассматривать вывод формулы Я. Бернулли в общем виде, нужно рассказать о повторных испытаниях и решить з а д а ч у:
1. Производится три независимых выстрела из оружия по мишени при условии, что вероятность попадания в мишень Р(А)=Р.
Найти вероятность того, что при этих выстрелах произойдет ровно два попадания.
В общем виде формула Я. Бернулли имеет вид 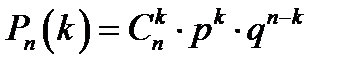 , где п— количество независимых опытов; к — количество опытов, в каждом из которых событие А осуществляется с вероятностью р и не осуществляется с вероятностью
, где п— количество независимых опытов; к — количество опытов, в каждом из которых событие А осуществляется с вероятностью р и не осуществляется с вероятностью 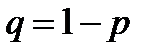 . Формулу Бернулли полезно вывести, так как в процессе вывода используются теоремы умножения и сложения вероятностей.
. Формулу Бернулли полезно вывести, так как в процессе вывода используются теоремы умножения и сложения вероятностей.
Теорема: Если вероятность p наступления события Α в каждом испытании постоянна, то вероятность 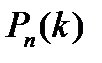 того, что событие A наступит k раз в n независимых испытаниях, равна:
того, что событие A наступит k раз в n независимых испытаниях, равна: 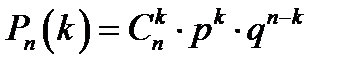 где
где 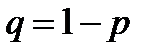
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|