ЛЕКЦИЯ 2. (2 часа).. Статистические гипотезы. Проверка статистической гипотезы о нормальном распределении с помощью критерия Пирсона χ2 . Элементы теории корреляции. Коэффициент корреляции. Линейная регрессионная модель.

ЛЕКЦИЯ 2. (2 часа).

Статистические гипотезы. Проверка статистической гипотезы о нормальном распределении с помощью критерия Пирсона χ2 . Элементы теории корреляции. Коэффициент корреляции. Линейная регрессионная модель.

Статистической называют гипотезу о неизвестном распределении или о параметрах неизвестного распределения.

Нулевой (основной) называют выдвинутую гипотезу H₀.

Конкурирующей (альтернативной) называют гипотезу H₁, которая противоречит гипотезе H₀.

Простой называют гипотезу, которая содержит одно предложение.

Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. В итоге проверки гипотезы могут быть допущены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза H₀. Вероятность ошибки первого рода называют уровнем значимости и обозначают буквой α. Ошибка второго рода состоит в том, что будет принята неправильная нулевая гипотеза H₀. Вероятность ошибки второго рода называют уровнем значимости и обозначают буквой β.

Статистическим критерием (или просто критерием) называют случайную величину K, которая служит для проверки гипотезы. Наблюдаемым (эмпирическим) значением критерия K_набл. называют то значения критерия, которое вычислено по выборке.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых нулевую гипотезу принимают. Критическими точками (границами) K_кр называют точки, отделяющие критическую область от области принятия гипотезы. Для отыскания критической области задаются уровнем значимости α и ищут критические точки из следующих соображений:

a) для правосторонней критической области (определяется неравенством K>K_кр, где K_кр>0) вероятность P(K>K_кр) = α;

b) для левосторонней критической области (определяется неравенством K<K_кр, где K_кр<0) вероятность P(K<K_кр) = α;

c) для двусторонней критической области (определяется неравенствами K<-K_кр, K>K_кр, где K_кр>0) вероятность P(K>K_кр) = α / 2, K_кр>0, и P(K<K_кр) = α / 2, K_кр<0.

Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то нулевую гипотезу принимают.

В математической статистике для проверки различных статистических гипотез применяются различные критерии: Колмогорова, Бартлетта, Кочрена, Спирмена, Пирсона и другие.

Для проверки гипотезы о нормальном распределении генеральной совокупности и различных параметров этого распределения обычно используют критерий Пирсона χ².

Пусть эмпирическое распределение (выборка) задано в виде последовательности (таблицы) равноотстоящих вариант и соответствующих им частот

x_i	x₁	x₂	…	x_k
n_i	n₁	n₂	…	n_k

Требуется, используя критерий Пирсона χ², проверить гипотезу H₀ о том, что генеральная совокупность X распределена нормально.

Для этого воспользуемся правилом A.

1. Вычислить непосредственно выборочную среднюю 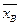и выборочное среднее квадратическое отклонение σ_B.

2. Вычислить теоретические частоты 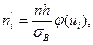где n – объем выборки, h – шаг,

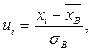
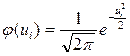3. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона χ². Для этого:

а) составляют расчетную таблицу, по которой находят наблюдаемое значение критерия

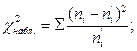
б) по таблице критических точек распределения χ², по заданному уровню значимости α и числу степеней свободы k=s-3 (s – число групп выборки) находят критическую точку 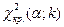правосторонней критической области.

Если 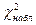< 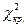, то нет оснований отвергать гипотезу H₀ о нормальном распределении генеральной совокупности. Другими словами, эмпирические и теоретические частоты различаются незначимо (случайно).

Если 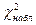> 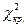, то гипотезу H₀ отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо.

Если эмпирическое распределение (выборка) задано в виде последовательности интервалов одинаковой длины и соответствующих им частот

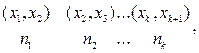
то следует воспользоваться правилом B.

1. Вычислить непосредственно выборочную среднюю 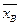и выборочное среднее квадратическое отклонение, 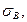причем в качестве вариант принимают среднее арифметическое концов интервалов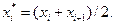

2. Пронормировать случайную величину X, то есть, перейти к случайной величине 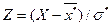и вычислить концы интервалов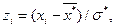 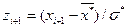, причем наименьшее значение Z, т.е. z₁, полагают равным – ∞, а наибольшее, т.е. z_k₊₁, полагают равным + ∞.

3. Вычислить теоретические частоты 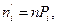где n – объем выборки, 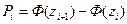– вероятности попадания X в интервалы 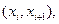а Ф(z) – функция Лапласа.

4. Сравнение эмпирических и теоретических частот с помощью критерия Пирсона χ² производится так же, как в пункте 3 правила A.

Две случайные величины X и Y могут быть связаны либо функциональной, либо статистической зависимостью, то есть такой, при которой изменение одной из величин влечет изменение распределения другой, либо независимы. Если две случайные величины X и Y независимы, то 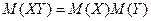, если же две случайные величины X и Y не являются независимыми, то, вообще говоря, .

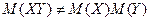Будем принимать за меру связи (зависимости) двух случайных величин X и Y безразмерную величину r, называемую коэффициентом корреляции и определяемую соотношением

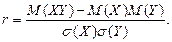
Некоторые свойства коэффициента корреляции r.

1. Если две случайные величины X и Y независимы, то r = 0, это означает, что случайные величины X и Y не коррелируют между собой, иначе, между ними нет связи.

2. Если две случайные величины X и Y зависимы, то r ≠ 0, что говорит о корреляционной зависимости случайных величин X и Y, причем, если r = 1 или r = -1, случайные величины X и Y связаны линейной зависимостью.

Корреляционная зависимость называется линейной корреляцией, если обе функции регресси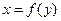и и 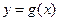линейные, при этом обе линии регрессии являются прямыми линиями регрессии. Общие уравнения прямых линий регрессии Y на X и X на Y имеют вид

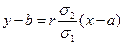и ,

где a = M(X), b = M(Y), , .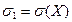

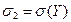Для выборочной совокупности уравнения прямых линий регрессии, соответственно, имеют вид

, ,

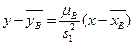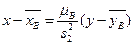где 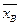, 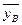– выборочные средние, 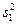, 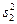– исправленные выборочные дисперсии случайных величин X и Y, .

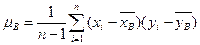На основе экспериментальных данных, статистических и других обследований часто строятся эмпирические формулы выявленных зависимостей. Одним из способов получения таких формул является метод наименьших квадратов.

Пусть проведено n независимых наблюдений случайной величины Y при значениях 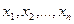величины X. При этом измерения случайной величины Y дали следующие результаты 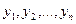. Предположим, что эти значения связаны линейной корреляцией Y на X, тогда эту связь можно выразить в виде линейной регрессионной модели

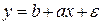где b, a – неизвестные параметры, ε – случайная ошибка измерений, причем .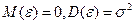

Задача линейного регрессионного анализа состоит в том, чтобы по результатам наблюдений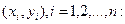

a) получить наилучшие точечные и интервальные оценки неизвестных параметров b, a и σ² модели;

b) проверить статистические гипотезы о параметрах модели;

c) проверить, достаточно ли хорошо модель согласуется с результатами наблюдений (адекватность модели).

Для определения неизвестных параметров b и a линейной регрессионной модели составляется так называемая нормальная система метода наименьших квадратов

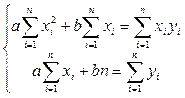Метод наименьших квадратов позволяет решать задачи криволинейного регрессионного анализа, то есть строить параболические, гиперболические, показательные и другие регрессионные модели.

Вопросы для самостоятельной подготовки по лекции 2.

1. Виды статистических гипотез.

2. В чем отличие правила А и правила В проверки статистических гипотез, используя критерий Пирсона χ².

3. Может ли быть значение коэффициента корреляции больше 2,5 для линейной модели.

ЛИТЕРАТУРА

1. Гмурман, В. Е. Теория вероятностей и математическая статистика : учеб. пособие - 12-е изд., перераб. М. : Высш. образование, 2008. - 479 с. - Г / МО.

2. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике : учеб. пособие 11-е изд., перераб. М. : Высш. образование, 2008. - 404 с. - (Основы наук). - Г / МО.

3. Кремер, Н. Ш. Теория вероятностей и математическая статистика : учебник / 3-е изд., перераб. и доп. М. : ЮНИТИ-ДАНА, 2007. - 551 с. - (Золотой фонд российских учебников). - Г / МО.

⇐ Предыдущая 12